WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Benadering ellips door cirkelbogen

Dit is een reactie op vraag 13823

Dit is precies de routine die ik ook bedacht had
Maar helaas, ik heb dit ook getekend in (in dit geval) AutoCAD, en daar bleek dat deze oplossing toch niet kan (!) . Dit blijkt als je het puur wiskundig bekijkt: een cirkel(-boog) kan niet worden bepaald door twee raaklijnen én tegelijkertijd door de twee opgegeven punten gaan.
Neem de punten net wat verder uit elkaar, en zoom in op een van beide punten, je zal zien dat er een 'gat' ontstaat.

Mark
Student hbo - vrijdag 29 augustus 2003

Antwoord

Dat klopt. Foutje.
Wat je zou kunnen doen is:
Je hebt het middelpunt M1 en het eindpunt P van de "vorige" cirkelboog.
De volgende cirkelboog eindigt in Q.
Je snijdt de lijn M1P met de middelloodlijn van PQ. Het snijpunt van deze lijnen is het middelpunt M2 van de voldende cirkelboog.
De boog PQ sluit in P continu aan op de vorige cirkelboog.
Op deze manier heb je dus voor elke boog 3 voorwaarden en ligt hij dus vast.

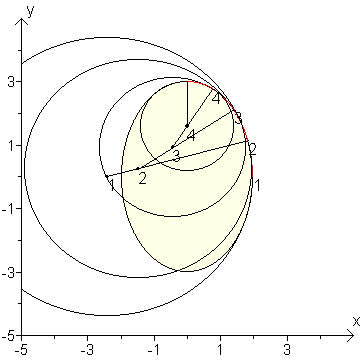
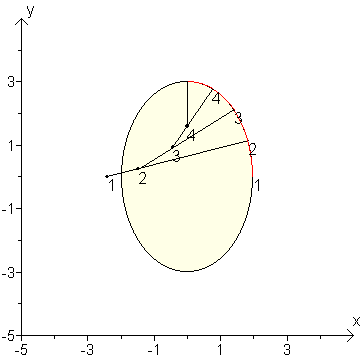
In onderstaande tekeningen ga ik uit van de ellips met halve lange as 3 verticaal en halve korte as 2 horizontaal. Ik heb voor de eerste cirkelboog (boog 12) als beginpunt (2,0) genomen en als middelpunt van de "vorige cirkelboog" (0,0). De ellips start zodoende netjes verticaal.
In rood zijn de berekende cirkelbogen aangegeven.

Voor sterk excentrische ellipsen moet je het aantal deelintervallen vrij groot nemen.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 31 augustus 2003