WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Nog eens... poissonverdeling

Gemiddeld gebeurt er op een weg elke 100 dagen een ongeluk. Het aantal ongelukken per maand (30 dagen) is poissonverdeeld.
Wat is de kans op 1 ongeluk per maand?
Wat is de kans dat tussen twee opeenvolgende ongelukken niet meer dan 3 dagen liggen?

Moest volgens mij zijn:
P(1 ongeluk per maand) = P(k = 1) met P(0.3), dat wordt
P(X1) - P(X0) = 0,963 - 0,741 = 0,222
Alleen zou dit niet kloppen (oplossing moet 0,0369 zijn :( ). Ziet iemand waar het probleem zit?
Voor het tweede deel heb ik echt geen idee hoe dat op te lossen. Is het mogelijk me op weg te zetten?
S
Student universiteit - donderdag 21 augustus 2003

Antwoord

1) Met je eerste antwoord lijkt mij niets mis, alleen zou ik het niet via de cumulatieve tabel doen. In de afzonderlijke tabel vind je die 0,222 direct terug.

2) Deze is lastiger. Het komt hier op neer: er is net een ongeluk gebeurt, wat is de kans dat er binnen 3 dagen weer een ongeluk gebeurt ?? Dat is 1 - de kans dat er binnen 3 dagen geen ongeluk gebeurt = 1 - kans op 0 ongelukken in 3 dagen.
De ellende is nog niet voorbij: de tabel helpt je namelijk niet omdat de bijbehorende verwachtingswaarde (m=0,03) niet in de tabel terug te vinden is. Dan moet je de formule van een poisson verdeling erbij pakken. Met die formule reken je uit P(K=0) bij Poissonverdeling met m=0,03:

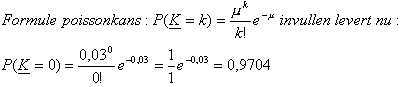
Het antwoord wordt dus uiteindelijk 1-0,9704=0,0296

Met vriendelijke groet

JaDeX

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 21 augustus 2003