WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Oppervlakte berekenen en inhoud berekenen

1.
gegeven is f(x)= (x²+4)/x
V is het gebied dat wordt ingesloten door de lijn y=5 en de grafiek van f.
Gevr.Bereken de oppervlakte.

Mijn oplossing: [.5x²+4.ln(x)] met grenzen 4 en 1 levert A=13 (bij benadering) maar dit schijnt niet correct te zijn maar waarom ?

2.
geg: f(x)=1/cosx, voor -$\pi$/2$<$x$<\pi$/2
F(x)=ln(1+sinx)/(cosx)
V is het gebied ingesloten door de lijn Y=√2) en de grafiek van f.
gevr: Bereken de inhoud van het lichaam dat ontstaat door V te wentelen om de x-as.

Ik weet niet hoe ik die formule om de inhoud te bereken hiervoor toe moet passen.

Graag uw reactie/uitleg
Mellaa
Leerling bovenbouw havo-vwo - dinsdag 19 augustus 2003

Antwoord

1.
Je hebt de oppervlakte van het rode gebied onder de grafiek berekend:

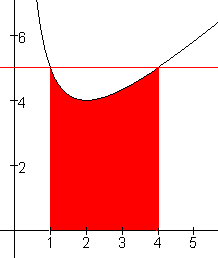
2.
Ik neem dat je de formule bedoelt uit dit overzicht:

vol(W)=$\pi\int{}$(1/cos(x))² dx
vol(W)=$\pi\int{}$(1/cos²(x)) dx

Let op: dit is dus wederom de inhoud van het stuk onder de grafiek... voor het stuk er boven moet je natuurlijk weer even kijken hoe of wat... (misschien kan het wel makkelijker), maar als het goed is herken je in 1/cos²(x) wel de afgeleide van tan(x)... zou het zo lukken!?
Zie Formulekaart

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 19 augustus 2003

Re: Oppervlakte berekenen en inhoud berekenen