WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Raaklijnen aan een parabool vanuit een gegeven punt

Hoe bereken ik een vergelijking van de raaklijnen vanuit (1,-3) aan de parabool: x²=8y
Charlo
Student hbo - vrijdag 15 augustus 2003

Antwoord

Bij dit soort problemen moet je altijd eerst even kijken op het punt (1,-3) wel op de parabool ligt (het makkelijke geval) of niet op de parabool ligt (het moeilijke geval). Uiteraard hebben we hier te maken met het moeilijke geval.

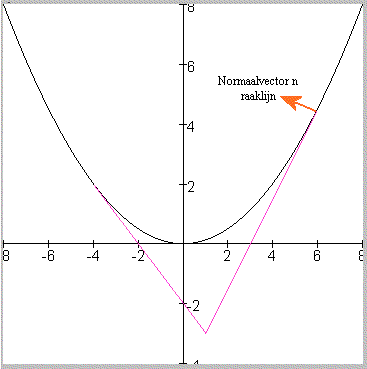
Dit moeilijke geval kan op verschillende manieren opgelost worden. Een uiterst fraaie oplossing is de volgende:
Schrijf eerst even de parabool als y=¹/₈x² (niet echt noodzakelijk)
De afgeleide is dan y'=¹/₄x (dus alg. richtingsvector raaklijn: (1,¹/₄x) )
Neem even aan dat het raakpunt algemene gedaante (x,y) heeft, dus raakpunt is (x,¹/₈x²)
Uit de afgeleide volgt de normaalvector in het raakpunt: n_v(¹/₄x,-1).
De richtingsvector van de lijn door het punt van de parabool en (1,-3)
is dan de richtingsvector door (x,¹/₈x²) en (1,-3) is r_v(x-1,¹/₈x²+3)
De genoemde normaalvector en de richtingsvector moeten loodrecht op elkaar staan dus moet het inproduct van deze vectoren 0 zijn.
Dat levert op ¹/₄x·(x-1)+ -1·(¹/₈x²+3)=0
Û¹/₄x²-¹/₄x-¹/₈x²-3=0 Û x²-2x-24=0 Û x=-4 of x=6

Zoals je kunt zien klopt dit. De raakpunten kun je nu makkelijk uitrekenen en die raaklijnen ook, je hebt tenslotte de normaalvector !!

met vriendelijke groet

JaDeX

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 15 augustus 2003