WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Driehoeken en cirkels

De tophoek van een gelijkbenige driehoek ABC meet 50°. De cirkel met middellijn [BC] snijdt AB in D en AC in E. Men verbindt het middelpunt O van deze cirkel met de punten D en E.
Bereken de grootte van de hoek DÔE.

Het lukt mij om de constructie op papier te zetten maar ik kom er niet uit welke formules te gebruiken om de hoek DÔE te berekenen.
de bis
3de graad ASO - woensdag 13 augustus 2003

Antwoord

Je vraag is nog niet helemaal duidelijk omdat ik niet weet welke hoeken je welke naam hebt gegeven. Daarom zal ik hier twee mogelijkheden bespreken.

Een aantal basisprincipes zul je moeten gebruiken:
- de hoeken van een driehoek zijn samen 180°
- de twee hoeken van de gelijkbenige driehoek zijn gelijk
- het middelpunt van de cirkel ligt op het midden van de middellijn.
- elk punt op een cirkel heeft dezelfde afstand tot het middelpunt.

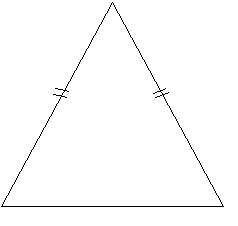
De driehoek die je beschrijft kun je als volgt tekenen. De tophoek is 50° en omdat de andere hoeken gelijk zijn, zijn beide andere hoeken dus (180°-50°)/2 = 65°

In de volgende twee plaatjes heb ik twee mogelijke situaties getekend (omdat ik niet helemaal wist wat bij jou de tophoek is). De lijnstukken die een gelijke lengte hebben in een tekening heb ik aangegeven.

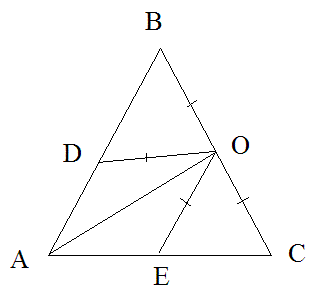
Ik zal alleen de gevraagde hoek uitreken als hoek B de tophoek is. De andere tekening kun je dan denk ik zelf wel berekenen.

ÐACB = 65° = ÐECO = ÐCEO
(omdat hier een gelijkbenige driehoek is ontstaan)
Dus omdat de hoeken van een driehoek samen 180° zijn geldt:
ÐBOD = 180° - 50° - 50° = 80°

ÐABC = 50° = ÐDBO = ÐBDO
(omdat ook hier een gelijkbenige driehoek is ontstaan)
Weer geldt dat de hoeken van een driehoek samen 180° zijn, dus:
ÐEOC = 180° - 65° - 65° = 50°

De hoeken die samen een hoek van 180° (rechte lijn) vormen zijn:
ÐEOC + ÐEOD + ÐDOB = 180°
dus ÐEOD = 180°-80°-50° = 50°

Ik hoop dat dit je vraag helemaal beantwoord. De andere driehoek kun je nu denk ik wel zelf.

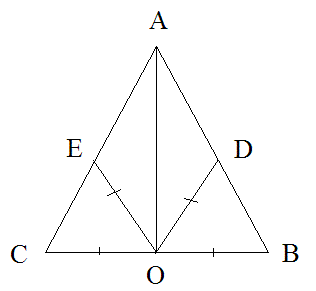
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 13 augustus 2003