WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Hoe moet ik nu verder?

De opdracht gaat als volgt:
'Een chocoladefabrikant maakt balkvormige repen die gevuld zijn met amarettopasta. De zijden hebben de drie binnenmaten: 5, 5 en 7 cm. De hoeveelheid chocolade die de fabrikant wil verwerken,is 19688 kubieke millimeter. Op alle zijvlakken is de dikte van de chocolalaag gelijk. Bepaal de dikte van de chocoladelaag.'

Nu heb ik die dikte de variabele x gegeven en kwam ik op deze vergelijking (ik heb de maten naar millimeters omgezet) :

(50+x)(50+x)(70+x) - 175000 = 19688
x³+7x²+9500x+175000-175000 = 19688
x³+7x²+9500x = 19688
hierna kom ik niet verder , de oplossing werd wel gegeven alleen geen uitleg, kunt u mij het uitleggen hoe het verder gaat, trouwens de oplossing: x = 2 mm

Man-Ch
Leerling bovenbouw havo-vwo - donderdag 7 augustus 2003

Antwoord

Hoi,

Je fout zit 'm in het uitwerken van de haakjes.
(50 + x)(50 + x)(70 + x) - 175000 = 19688
(50 + x)²·(70 + x) = 194688
(2500 + 100x + x²)·(70 + x) = 194688
2500·70 + 2500·x + 100x·70 + 100x·x + x²·70 + x²·x = 194688
x³ + 170x² + 9500x + 175000 = 194688
x³ + 170x² + 9500x - 19688 = 0

Dit gaan we ontbinden in factoren door x³ + 170x² + 9500x - 19688 gelijk te stellen aan een functie, zeg f(x). Nu zijn er twee mogelijkheden: de Euclidische deling óf het schema van Horner (hoewel deze methodes vrijwel analoog zijn).

Euclidische deling
Schrijf de delers van de constante term op. In ons geval dus de delers van -19688, dus ±1, ±2, ±4, ±8, ...
Daarna gaan we kijken welke deler de nuldeler is, dus het nulpunt van de functie (indien deze er is uiteraard).
Het blijkt dat f(2) = 0. We gaan f(x) delen door x - 2.

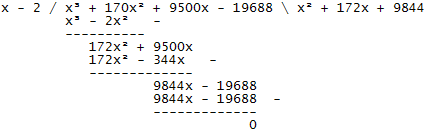
De rest is 0 en [x³ + 170x² + 9500x - 19688]/[x - 2] = x² + 172x + 9844 + ⁰/_{(x - 2)} = x² + 172x + 9844
En hieruit volgt (kruisproduct) dat f(x) = (x - 2)(x² + 172x + 9844). Ter controle kunnen we deze functie uitwerken, je zult zien dat je de originele functie uitkomt. En hiervan (is) zijn (het) de nulpunt(en) niet moeilijk te berekenen, want een product is nul dan en slechts dan als één van de factoren nul is, dus (x - 2) = 0 Ú (x² + 172x + 9844) = 0
Þ x = 2 Ú (x² + 172x + 9844) = 0
D = b² - 4ac = 29584 - 39376 = -9792
D 0 Þ geen reële oplossingen

Dus x = 2 is het enige (reële) nulpunt.

Schema van Horner
Je moet weer de nuldeler vinden zoals hierboven beschreven. De nuldeler was x = 2. Schrijf deze nuldeler linksonder in het schema. Helemaal boven in het schema schrijf je de coëfficiënten van f(x) waarbij de graad van de termen dalend is gerangschikt; indien er een term ontbreekt schrijf je 0. Je begint bij de eerste coëfficiënt, die schrijf je onder de streep en vermenigvuldig je met de nuldeler en het product schrijf je onder de tweede coëfficiënt, je telt de tweede coëfficiënt op met het product en de som schrijf je onder de streep. Nu herhaal je de procedure totdat je de laatste plek hebt ingevuld. Je ziet dat er rechtsonder een 0 uitkomt, dat is je rest. Links van de nul gezien staat de constante van de ontbonden functie, weer een plaats naar links de eerstegraadsterm, dààrvoor de tweedegraadsterm, enz. Zie onderstaand schema.

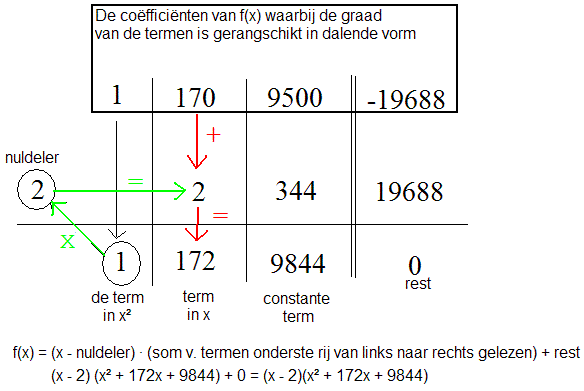
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 7 augustus 2003