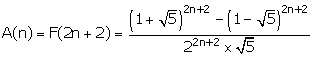|
|
|
\require{AMSmath}



Wandelingen langs pijlen
Ik heb een figuur:
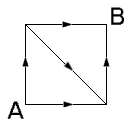
Als je dit figuur N keer achter elkaar plakt zoiets als dit:
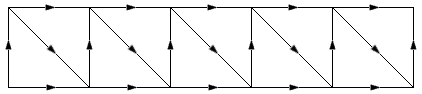
...en als je dan in de richting van de pijlen van a naar b loopt wat is dan de formule om uit te rekenen hoe veel mogelijkheden er zijn (deze som stond in ons 2e klassers vwo boek maar ook onze leraren kwamen er niet uit)?
chris
Leerling onderbouw vmbo-havo-vwo - dinsdag 5 augustus 2003
Antwoord
Om achter de formule te komen kan je bij de 'hoekpunten' eens het aantal mogelijkheden zetten:
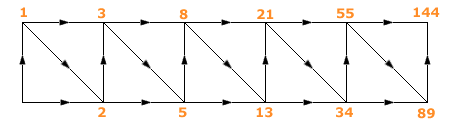
...en die getallen komen 'ons' bekend voor!
We stellen vast dat bij 5 vierkantjes het aantal mogelijkheden gelijk is aan Fib(12).
Even een tabel:| n | A(n) | | 1 | Fib(4) | | 2 | Fib(6) | | 3 | Fib(8) | | 4 | Fib(10) |
| 5 | Fib(12) |
Dus... voor n vierkantjes zijn er Fib(2n+2) mogelijke wandelingen. Omdat we de formule voor Fib() al kennen zou je als formule kunnen schrijven:
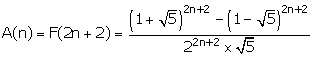
..en dat lijkt me zelfs voor een tweedeklasser wel een beetje al te gek!
Meer weten over de rij van Fibonacci? Zie Fibonacci/Guldensnede.
Zie ook: Fibonacci en de driehoek van Pascal

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 5 augustus 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|