WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Bivariate normaalverdeling/SPSS/dringend hulp gevraagd

Beste wiskundeknobbels,

Om de Pearson's correlatiecoëfficiënt te gebruiken, zijn er een aantal voorwaarden waar aan voldaan moet worden. Een van de voorwaarden is dat de steekproef afkomstig moet zijn uit een bivariate normale verdeling. Dus voor elke waarde van bv.variabele x₁ moet variabele x₂ normaal verdeeld zijn. Kan iemand mij aub uitleggen hoe ik dit met behulp van SPSS kan nagaan?
(Veel) dank bij voorbaat!
Koen

koen
Student universiteit - zondag 3 augustus 2003

Antwoord

Een bivariate normale verdeling ziet er als volgt uit:

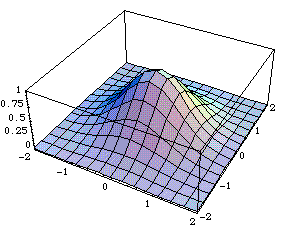
Om te controleren of een verdeling bivariaat normaal is, is het niet voldoende om te toetsen of voor elke waarde van variabele x₁ de variabele x₂ normaal verdeeld is. Bovendien zou deze toets nooit werken wanneer al je x₁ en x₂ waarden grotendeels verschillend zijn. Hiemee kom je er dus niet. Wat kun je dan wel doen ?
Als een verdeling van punten (x₁,x₂) bivariaat normaal verdeeld is dan is het automatisch zo dat de scores x₁ en x₂ dan ook normaal verdeeld zijn. Derhalve wordt vaak volstaan met dit laatste te toetsen. Met SPSS kan dat met de toets van Kolmogorov-Smirnov (KS-Lillyfors) of de toets van Shapiro-Wilks. Wiskundig gezien is dit niet helemaal correct. Bovenstaande bewering mag namelijk niet omgekeerd worden: Als scores x₁ en x₂ beiden normaal verdeeld zijn is het NIET automatisch zo dat de punten (x₁,x₂) ook een bivariate normale verdeling volgen. Wanneer dit echter inderdaad misgaat heb je wel te maken met hele vreemde verbanden tussen x₁ en x₂, die je in de praktijk zo een twee drie niet tegen zal komen.
Naar mijn weten is het onderzoek naar toetsen op bivariate normale verdelingen kort geleden pas gestart. Het zou kunnen dat je hierover wat terug kunt vinden bij de wiskundigen Mardia en Looney. De toets voor controle van een echte bivariate normale verdeling ben ik in SPSS derhalve nog niet tegengekomen. Ik adviseer je dus de toets van KS of SW (zelf even nazoeken) met toevoeging van de bovenstaande opmerking.

Met vriendelijke groet

JaDeX

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 4 augustus 2003