WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Buigpunten

Hallo,

Ik moet de buigpunten zoeken van deze twee volgende functies dit doe ik zo eerst bepaal ik de afgeleide dan de tweede deze stel ik gelijk aan nul hier uit haal ik x.

Nu zegt men mij (in de oplossingen ) dat de eerste functie hier onder geen buigpunt heeft eerst dacht ik dan als x gelijk is aan nul dan heeft de functie geen buigpunt nu de tweede functie zijn x ook gelijk aan nul en deze heeft toch ook een buigpunt? (dat deze een buigpunt heeft staat ook in de oplossingen)

Nu is mijn vraag hoe kan ik weten dat een functie een buigpunt heeft of niet?
H(x)=x⁴+1
H’(x)=4x³
H’’(x)=12x²

12x²=0
x=0
y=1

M(x)=¹/₄x³+x-2
M’(x)=³/₄x²+1
M’’(x)=1¹/₂x

1¹/₂x=0
x=0
y=-1

Dank bij voorbaat.
Bert F
3de graad ASO - zaterdag 2 augustus 2003

Antwoord

Het 'feit' dat de tweede afgeleide nul is in een punt is nog geen voldoende voorwaarde voor het 'buigpunt' zijn. Als bijkomende eis komt daarbij dat de tweede afgeleide van teken wisselt.

Ga maar na! Wat is een buigpunt? Een buigpunt is een punt van de grafiek waar de richtingscoëfficiënt van de raaklijn (de afgeleide) een minimum of maximum bereikt!

Hoe onderzoek je of een functie een minimum of maximum bereikt? Door de afgeleide te nemen (in dit geval de afgeleide van de afgeleide = de tweede afgeleide), nul stellen en een tekenverloop te maken. Het is immers mogelijk dat de afgeleide weliswaar nul is, maar dat er geen sprake is van een buigpunt.

Voorbeeld
De functie f(x)=x⁴+1

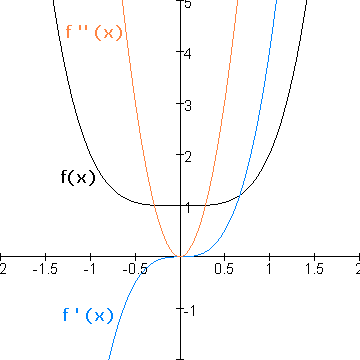
f''(x) is inderdaad 0 voor (0,1). Maar zoals je ziet heeft de afgeleide (de blauwe grafiek) daar geen minimum of maximum, maar een buigpunt, dus is (0,1) (in de oorspronkelijke grafiek) geen buigpunt.

Hoe kom je daar achter zonder de grafiek te tekenen? Zoals je het gedaan hebt is het ok, maar maak dan nog even een tekenverloop van de tweede afgeleide:

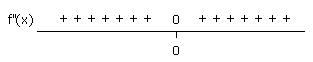
Conclusie: De tweede afgeleide wisselt niet van teken dus bij x=0 geen buigpunt.

Voorbeeld 2
Zie boven M.
Allemaal goed...
Tekenverloop M''(x):

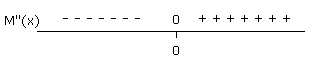
Nu bereikt de afgeleide inderdaad een minimum, dus is er in (0,-2) inderdaad sprake van een buigpunt.

Kijk maar in de grafiek:

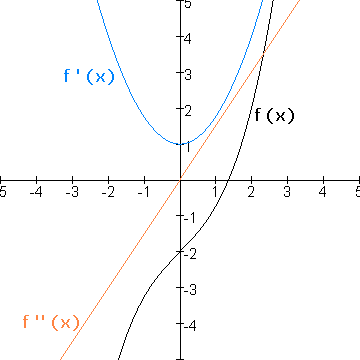
De tweede afgeleide wisselt van teken, de afgeleide (blauwe grafiek) heeft een minimum... dus een buigpunt.
Zie Meer voorbeelden....

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 2 augustus 2003

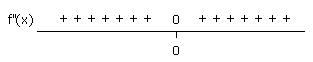
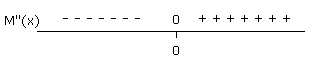
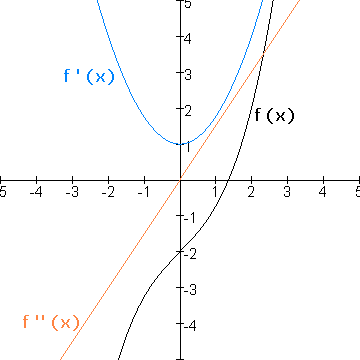
Re: Buigpunten