WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Asymtoten en extremen berekenen

Beste wisfaq,

(1) Hoe vind men de asymtoten van f(x) met behulp limieten ?

f(x)= (x-1)/(x+1)²

ik heb me laten vertellen dat ze dit doen door de
limiet van x¯-1 en lim x-1 nemen om de verticale asymtoot te berekenen, maar hoe komen ze aan die -1 ? En hoe gaat het precies ?

(2)Dan wordt er gevraagd om de extremen te bepalen, dan weet ik dat men de afgeleide moet berekenen en gelijkstellen aan o, maar moet men de teller EN de noemer gelijkstellen aan o of alleen de teller ?

(3) Dit vraag ik omdat ik de functie:

g(x)= (2Öx)/(x+1) moet differentieren en de extreme waarden moet vinden.
Timmy
Leerling bovenbouw havo-vwo - donderdag 17 juli 2003

Antwoord

(1)
De functie heeft (twee keer) de factor x+1 in de noemer. De functie bestaat daardoor niet als x + 1 =0 (deling door 0).
Vandaar dat het nodig is te kijken naar limieten voor x¯-1 en voor x-1.
>
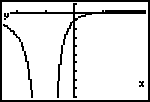
In beide gevallen wordt de noemer (positief) erg klein, nadert tot 0.
De teller nadert tot -2.
De limiet is dan -¥ (negatief erg groot).
Dus is x = -1 een verticale asymptoot (zie plaatje).

(2)
Voor het onderzoek naar extremen gebruik je van de afgeleide:
TELLER = 0.
Daarna onderzoek je of voor de gevonden waarde(n) van x de noemer (van de afgeleide) ONGELIJK aan 0 is.
Is dit het geval, dan is er meestal (!) een extreme waarde.
Je kan dat zien aan het tekenschema van de afgeleide in de buurt van zo'n nulpunt van de teller.
Er moet tekenwisseling van de afgeleide optreden!

(3)
Voor de gegeven functie geldt:
g'(x) = T/N
met T = 1/(Öx) * (x+1) - 2Öx * 1
T = 0 geeft (na vermenigvuldiging met Öx):
x + 1 - 2x = 0
zodat x = 1
Voor N (van de afgeleide) hebben we N = (x+1)²
Voor x = 1 geldt N ¹ 0.
Het tekenschema van g' is in de buurt van x = 1:
++++0----
Er is dus sprake van een maximum g(1) = 1.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 17 juli 2003