|
|
|
\require{AMSmath}
Transformatie van 3-dimensionale euclidische ruimte
Ik heb 2 cartesiaanse assenstelsels, 1 vast en 1 dat kan bewegen oorsprong vallen samen (zodat de punten allemaal vast liggen tov het referentie assenstelsel).
Om nu deze punten terug om te zetten naar het vaste assenstelsel kan men zijn coördinaten vermenigvuldigen met een matrix. Wat is deze matrix? het referentie assenstelsel kan roteren in de 3 richtingen tov de oorsprong
ik kom momenteel als volgt uit
X= cos \beta·cos\gamma·x + cos\beta·sin\gamma·z + sin \beta·y
Y= (-cos\alpha·sin\beta·cos\gamma-sin\alpha·sin\gamma)·x
+(cos\alpha·cos\beta)y
+( -cos\alpha·sin\beta + sin\alpha·cos\gamma)
Z= (sin\alphasin\betacos\gamma- cos\alphasin\gamma)·x
+(-sin\alpha·cos\beta)·y
+(sin\alphasin\betasin\gamma+cos\alpha·cos\gamma·z
(eerst heb ik de Hoek in YZ genomen dan die in XY en dan XZ)
klopt mijn resultaat en/of kan dit niet eenvoudiger , aangezien ik er van uitga dat de volgorde van de keuze van de hoeken niet uitmaakt waardoor je een symetrische matrix zou bekomen?
Vraag: Optimale Matrix
tom le
Student Hoger Onderwijs België - dinsdag 8 juli 2003
Antwoord
Het ziet er vrij goed uit. Alleen wordt conventioneel een andere volgorde gebruikt:
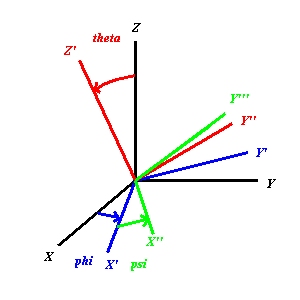
Het bijgevoegd pfd-bestand geeft de analytische uitwerking.
Koen Mahieu
Zie Kinematische vergelijkingen van Euler
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 8 juli 2003
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|
Re: Transformatie van 3-dimensionale euclidische ruimte