WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Opgaven met kromme

Dit is een reactie op vraag 12959

Als ik het het volgende commando in Maple geef:
plot([(1/4)*t^2-3*t,(t+4/t)-5,t=0..infinity],x=-10..10,y=-2..10);

dan wordt de tekening wel correct getekend.
Eelco
Leerling bovenbouw havo-vwo - woensdag 2 juli 2003

Antwoord

Ja dat klopt wel. Maar wat jij schreef was t/4 ipv 4/t.

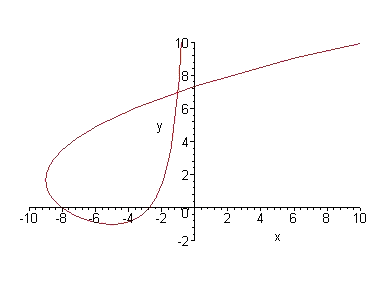
Dus nu hebben we de opgave al. Even zoeken naar een antwoord.

a) wat hebben we nodig. De t-waarde voor x=0 en de afgeleide van y naar x in die t-waarde. Dan hebben we de richtingscoefficient. Als we daar de Arctan van nemen hebben we het antwoord, toch?
Even praktisch: x=0 komt overeen met 1/4t²- 3t =0

Dus t=0 of t=12
t=0 kan niet van dan is de y-waarde +¥ en dat is geen snijpunt.

Dus t=12

leid y(t) af naar x en beschouw dit in het punt t=12:
dy/dx=dy/dt·dt/dx .Anders dy/dx = dy/dt : dx/dt
in t=12
=> dy/dx(12)=35/108
arctan(35/108)= 0.3133 in radialen
in graden: 18°

b) Het punt (-1,7) moet twee positieve t-waarden hebben het stelsel:

-1=1/4t²-3t
7=t+4/t-5

Moet dus twee oplossingen hebben voor t of hetzij één oplossing met multipliciteit 2

Dat is zo. Los het stelsel maar eens op. Je zult zien dat de t-waarde 3+22 een multipliciteit 2 heeft.

Koen Mahieu

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 2 juli 2003