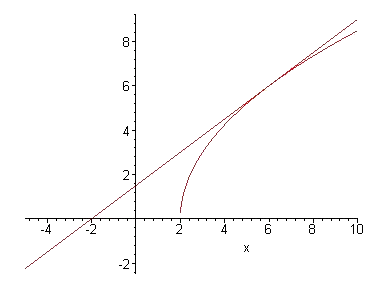WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Oppervlakte bepalen

geg: f(x)= 3√x-2 , l(x)= 3/4x+1.5

Gevr. V is het vlakdeel dat wordt ingesloten door de grafiek van f, de x-as en lijn l.Bepaal de oppervlakte van V

Deze opgave lukt mij niet echt ik weet wel hoe het moet alleen krijg ik andere antwoorden dan wat er in mijn antwoorden boek staat.

Zo ga ik f(x)=l(x)gelijk stellen om te weten te komen op welk interval te integreren dan krijg ik als uitkomst 5,7 (afgerond) maar mijn GRM zegt 6 dan neem ik aan dat ik iets verkeerd doe met mijn vergelijking en ga verder met 6...dan ga ik integreren:

-2 tot met 6 3/4x+1,5 -(3√x-2)dx

L(x)= (3/4).¹/₂x² + 1,5x
F(x)=2(x-2)√x-2 na het invullen krijg ik 11 als antwoord terwijl het antwoordenboek 8 als antwoord drukt weet u misschien wat ik verkeerd doe ? Kunt u dit misschien in kleine stapjes laten zien zodat ik kan zien wat ik verkeerd heb gedaan?

Bijvoorbaat dank
Hamble
Leerling bovenbouw havo-vwo - woensdag 2 juli 2003

Antwoord

de functies:

f:= x$\to$ 3√(x-2)
l:= x$\to$ 3/4x+3/2

Je kan best de figuur eens maken:

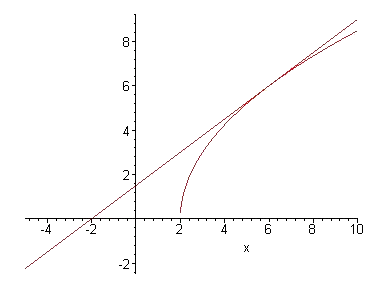
Je kan nu de grenzen aflezen. Er wordt gevraagd de opeervlakte tussen beide krommes en boven de X-as te bepalen. Je ziet duidelijk dat de grenzen voor f(x) [2,6] zijn en die voor l(x) [-2,6]

Dat snijpunt 6 vind je door f(x) en l(x) aan elkaar gelijk te stellen en op te lossen naar x.

f(x)=l(x)
3√(x-2)=3/4x+3/2
9(x-2)=9/16x²+2·3/2·3/4·x+9/4
9/16·x²-27/4·x+81/4= 0
Na oplossen met abc-formule volgt een wortel x=6 met multipliciteit 2

De integralen zou je zelf moeten kunnen. Je berekent dus
$\int{}$l(x) dx - $\int{}$f(x) dx
tussen de gegeven grenzen

De uitkomst is 8

Koen Mahieu

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 2 juli 2003