WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

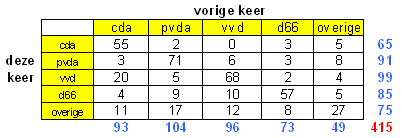
Verkiezingen

Als je twee opeenvolgende verkiezingen voor de 2de Kamer met elkaar vegelijkt, dan zie je dat mensen regelmatig veranderen van partij. Aan 415 Nederlanders die beide keren hebben gestemd is gevraagd op welke partij dat was. De gegevens staan in de tabel. Overige is 1 partij!
 
                       Vorige keer 
             cda   Pvda   vvd   d66   Overige 
deze     cda 55      2     0     3       5 
         pvda 3      71    6     3       8 
keer     vvd  20     5     68    2       4 
         d66  4      9     10    57      5  
     Overige  11     17    12    8       27 
vraag: bereken in vier decimalen nauwkeurig de kans dat een willekeurig gekozen ondervraagde
de vorige keer op het cda stemde.. 3/415 maar hoe kom je hieraan?
deze keer op de pvda stemde ... 1/415 maar hoe kom je hieraan?
weer op zijn eigen partij stemde... 8/415 maar hoe kom je hieraan?
die de vorige keer opd e pvda stemde nu op het cda stemde.. 2/415.. maar hoe kom je hieraan?
die de vorige keer op d66 stemde nu op een andere partij stemde... 6/415 maar hoe kom je hieraan?

alvast bedankt
marlij
Leerling bovenbouw havo-vwo - zondag 22 juni 2003

Antwoord

Volgens mij klopt er van het antwoordenboekje niet veel.

De tabel:

Bereken in vier decimalen nauwkeurig de kans dat
een willekeurig gekozen ondervraagde de vorige keer op het cda stemde...

Antwoord: ⁹³/₄₁₅ (kolom cda)

...deze keer op de pvda stemde ...

Antwoord: ⁹¹/₄₁₅ (rij pvda)

....weer op zijn eigen partij stemde...

Antwoord: ²⁷⁸/₄₁₅ (diagonaal)

...die de vorige keer op de pvda stemde nu op het cda stemde..

Antwoord: ²/₁₀₄ (kolom pvda)

...die de vorige keer op d66 stemde nu op een andere partij stemde...

Antwoord: ¹⁶/₇₃ (kolom d66)

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 22 juni 2003