|
|
|
\require{AMSmath}



Inhoud torus
Ik snap nie hoe je bij de bereking van de inhoud van een torus tot die twee integralen komt die je dan moet aftrekken.
koen
3de graad ASO - zondag 15 juni 2003
Antwoord
Hoi,
Ik zal je een opgave uit Moderne Wiskunde B1 deel 5 van Wolters Noordhoff (pagina 57, opgave G-6) stap voor stap uitleggen. Indien er dan nog moeilijkheden zijn met jouw opgave(n) stel je gewoon een nieuwe vraag.
Beschouw een cirkel met middelpunt (0,4) en straal 2.
Indien je deze om de x-as wentelt onstaat er een torus.
Stel functievoorschriften voor het bovenste en het onderste deel van de cirkel en bereken de inhoud van de torus.
Functievoorschrift opstellen voor bovenste gedeelte
Het algemene functievoorschrift voor 'n halve cirkel is f(x) = Ö[straal2 - x2]
Hier heeft het bovenste gedeelte dus de functie f(x) = Ö[4 - x2]. Maar dan krijg je een grafiek die 'op' x-as ligt, en het middelpunt moet (0,4) zijn, dus moet de functie 4 eenheden naar boven verschoven worden, dus wordt de functie f(x) = Ö[4 - x2] + 4.
Functievoorschrift opstellen voor onderste gedeelte
Als je opnieuw vertrekt van de opgestelde functie die 'op' de x-as ligt, kun je een functievoorschrift voor het onderste gedeelte opstellen door de bovenste functie te spiegelen in de x-as, waardoor alle waarden negatief worden, waardoor je de functie -Ö[4 - x2] krijgt, maar het middelpunt moet (0,4) worden dus moet deze functie ook weer 4 eenheden naar boven verschoven worden, waardoro je g(x) = -Ö[4 - x2] + 4 krijgt.
Inhoud torus berekenen door omwenteling x-as
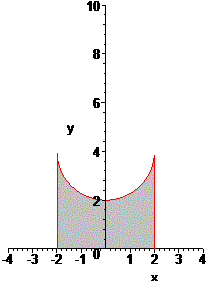
Om nu de inhoud van de torus te berekenen, wentelen we eerst het bovenste gedeelte van de cirkel om de x-as, krijgen we
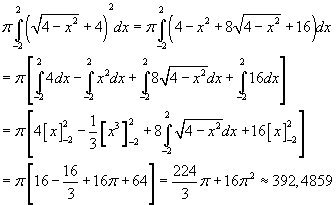
Nu hebben we eigenlijk dit gebied omgewenteld.
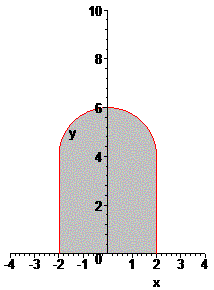
Maar dat is te veel! Het onderste gedeelte moet niet omgewenteld worden. In onderstaand plaatje zie je welk gedeelte moet worden omgewenteld (om x-as) en van vorige antwoord moet worden afgetrokken.
Berekening
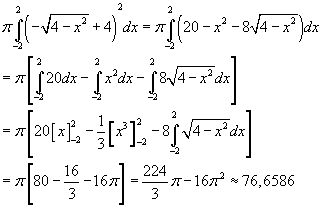
Dus de inhoud van torus is (224/3p + 16p2) - (224/3p - 16p2) = 32p2  315,8273409 315,8273409

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 15 juni 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








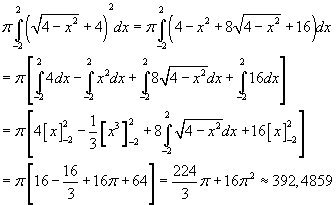


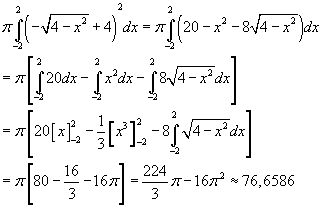
 315,8273409
315,8273409

