WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Numerieke wiskunde / Trapeziumregel

I=integraal van: getal e tot de macht sin(x) met interval [0 1]
Nu moet ik met de gerepeteerde trapeziumregel de absolute fout uitrekenen, I· 1, I·2, I·3, I·4 en I·100.
Hier kom ik absoluut niet uit, weet niet hoe ik dit aan moet pakken.
Ik moet iets doen met de 2e afgeleide, daar kom ik nog wel uit en dan... alleemaal zeer vage stof voor mij.
Hopelijk kunnen jullie me helpen.
Een zeer wanhopige docente van 41 jaar die bijna klaar is met 2e graads opleiding.
Sidone
Docent - zaterdag 14 juni 2003

Antwoord

Gegeven f(x) = e^sin(x) op het domein [0,1]

I₄ is de schatting van de integraal van deze functie op het stuk van [0,1] door toepassing van de herhaalde trapeziumregel (in dit geval 4 keer).

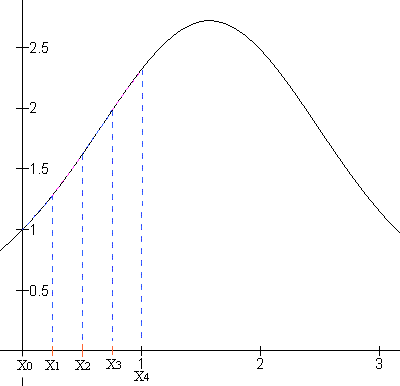
Zoals je ziet benadert de oppervlakte van de 4 trapezia (gekleurde stippellijnen) de integraal van de oorspronkelijke functie (zwarte grafiek) behoorlijk goed.
De oppervlakte van het eerste trapezium is ¹/₄·[{f(x₀)+f(x₁)}/2].
Voor alle trapezia samen wordt de totale opppervlakte:
¹/₄·¹/₂·{f(x₀)+2f(x₁)+2f(x₂)+2f(x₃)+f(x₄)}=
¹/₄·¹/₂·{1 + 2·1,28 + 2·1,62 + 2·1,98 + 2,32} = 1,63321.

Hoe groot is nu de fout in deze schatting ?? Daar is een formule voor:

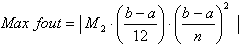
Hierin is M2 het maximum van de absolute waarde van de tweede afgeleide van de oorspronkelijke functie. Dit maximum bedraagt 1,2748 (bij x=1).
a en b zijn respectievelijk de beginwaarde en eindwaarde van het interval waarop je integreert dus a=0 en b=1.
n is het aantal keren dat je herhaald de trapeziumregel toepast (nu 4 dus).
Invullen levert op 0,00664 voor de maximale fout in de bovenstaande schatting.

Die tweede afgeleide is hier f"(x)=(cos²(x)-sin(x))·e^sin(x)
Dat maximum van de absolute waarde van die tweede afgeleide is overigens (zoals ook hier) niet altijd makkelijk te vinden. Dat daar 1,2748 uitkomt kun je afleiden door te laten zien dat de tweede afgeleide altijd daalt. Dat is lastig!

Wat je in dit soort gevallen altijd kunt doen is afschatten:
cos²(x)-sin(x) = 1 - sin²(x) - sin(x) is altijd dalend op [0,1]
dus voor cos²(x)-sin(x) geldt maximum 1 en minimum -0,55
e^sin(x) is altijd stijgend op [0,1] met minimum 1 en maximum 2,32.
Dat betekent dat de absolute waarde van de tweede afgeleide (dus M2) dan in ieder geval nooit groter kan zijn dan 2,32.

Bij de I₁₀₀ krijg je bij de benaderingsformule natuurlijk 1/100 in plaats van 1/4. Verder blijft die maximale absolute waarde voor die tweede afgeleide gelukkig wel hetzelfde. Nou zo zou de rest toch wel moeten lukken nietwaar?

Met vriendelijke groet

JaDeX

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 14 juni 2003

Numerieke wiskunde