WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Voorkomens in reeksen (complexe eigenschappen)

Stel, ik heb een zo'n automaat van de lotto met balletjes erin. Deze zijn genummerd van 1 tot en met N. Ik trek F maal een balletje, schrijf het nummer op en stop hem onmiddellijk terug! (trekken met terug leggen dus).

Na de F trekkingen met terugleggen bekijk ik de reeks die ik heb opgeschreven. Ik tel nu het aantal nummers dat eenmalig voorkomt, het aantal nummers dat twee keer voorkomt, etc. Wat zijn de verwachtingswaarden van deze aantallen?

Als voorbeeld geef ik F=2 keer trekken met N=2 balletjes. De mogelijke configuraties zijn:
bal 1, bal 2
1 1
1 2
2 1
2 2
In de eerste trekking zitten 0 eenmalige nummers en 1 tweemalig nummer
In de tweede trekking zitten 2 eenmalige nummers en 0 tweemalige nummers
In de derde trekking zitten 2 eenmalige nummers en 0 tweemalige nummers
In de vierde trekking zitten 0 eenmalige nummers en 1 tweemalige nummer.

Het totaal eenmalige nummers is dus 4 en het totaal tweemalige nummers is 2. De verwachte hoeveelheid eenmalige nummers bij F=2 trekkingen uit N=2 ballen is gelijk aan 4/4 = 1. De verwachte hoeveelheid tweemalige nummers bij F=2 trekkingen uit N=2 ballen is gelijk aan 2/4 = 1/2.

Dus tellen lukt dit wel. Maar hoe reken ik dit uit bij F=20 grepen uit N=20 ballen!?? Kortom, wat is de generieke formule (met als input x (aantal dezelfden), F (aantal grepen) en N (aantal ballen)) die deze getallen geeft?

Michie
Iets anders - vrijdag 13 juni 2003

Antwoord

Hoi,

Dat is een pittige vraag die je stelt. Vooraf waarschuw ik maar alvast dat er geen eenvoudige formule gegeven kan worden. Je zult dus flink moeten rekenen! Voor kleine F-waarden valt dit nog mee, maar als F groter wordt kan het rekenwerk behoorlijk omvangrijk en ingewikkeld worden... Weet waar je aan begint img src='smile.gif' align='absmiddle'

Eerst nog een opmerking over je voorbeeld. De verwachtingswaarde van het aantal eenmalige nummers is daar inderdaad 1, maar dit bereken je formeel door: kans op gebeurtenis * waarde gebeurtenis = kans op 2 enkelvoudige getallen * 2 = sup1/sup/sub2/sub*2 = 1

Dan nu voor het algemene geval. De verwachtingswaarde bereken je als volgt: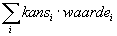

Nu eerst alle kansen uitrekenen... Hieronder is x het aantal verschillende getallen dat getrokken wordt:

Goed, nu kan de formule voor de verwachtingswaarde ingevuld worden. Let er hier bij op welke kansen er allemaal meegenomen moeten worden! Een en ander is uitgewerkt in een voorbeeld voor F=5 en N=10. Hier berekenen we weer eerst de kansen en daarna de verwachtingswaarden:

Zoals je ziet moet je dus goed opletten welke combinaties er mogelijk zijn. Voor elke combinatie moet je afzonderlijk de kans berekenen. En zoals gezegd, als het aantal getallen groter wordt, wordt ook het aantal combinaties groter en neemt het rekenwerk behoorlijk toe!

Succes,

Erica

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 23 juni 2003