WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Benaderen van sin x

Hoe kan ik laten zien dat deze reeks:

x - (x^3/3!) + (x^5/5!) + (x^7/7!) + (x^9/9!) - ...

sin x benadert?
Iris v
Leerling bovenbouw havo-vwo - zaterdag 7 juni 2003

Antwoord

Hoi,

Die reeks is ontstaan door de reeksontwikkeling van Taylor toe te passen (rond het punt 0). Je kunt nagaan dat dit een goede benadering is door bijvoorbeeld waarden voor x te nemen waarvan je eerst de sinus neemt, en daarna die x invult in de reeks. Komt er nagenoeg hetzelfde uit dan klopt de benadering. Maar dan klopt 't maar voor één waarde van x. Controleren of 't voor meerdere waarden geldt kun je doen door een plotje te maken van sin(x) en de reeksontwikkeling en kijken of die overeenkomen (het geldt dan voor dat specifieke interval).

Bijvoorbeeld

Jouw gegeven reeksontwikkeling is niet 100% correct.
De vierde term moet namelijk negatief zijn (afwisselend positieve en negatieve termen tot de restterm, die is altijd positief). Als we de sinusfunctie en de reeksontwikkeling x - ¹/₆x³ + ¹/₁₂₀x⁵ - ¹/₅₀₄₀x⁷ + ¹/₃₆₂₈₈₀x⁹ + O(x¹¹) in één plaatje plotten op het interval [-2p,2p] dan zie we hetvolgende (de groene grafiek is sin(x) en de rode de reeksontwikkeling).

Wat zie je? De ontwikkeling is een goede benadering rond x Î [-4,4], maar daarbuiten niet.

Als we sin(x) beter gaan benaderen, dus met meer termen gaan benaderen, krijgen we bijvoorbeeld

En als we die functie plotten krijgen we

Die functie benadert de sinusfunctie op 'n groter interval, en als je dit blijft herhalen en de reeksontwikkeling naar oneindig laat gaan, valt de grafiek van sinus en de reeksontwikkeling samen. En via dezelfde manier kun je ook een bepaalde waarde van de sinus berekenen door onderstaande reeks.

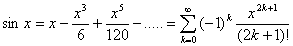
Groetjes,

Davy.

Zie bijvoorbeeld deze pagina

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 7 juni 2003

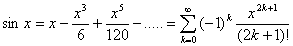
Re: Benaderen van sin x