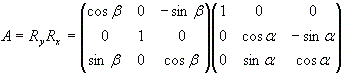WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Rotatie in een 3D ruimte

Dit is een reactie op vraag 12002

Alvast bedankt voor je antwoord. Een kant-en-klare formule was een beetje utopisch?

Hoe bepaal je die rotatie-matrix A? Zijn er niet verschillende mogelijkheden?

Olivie
Iets anders - vrijdag 6 juni 2003

Antwoord

Je hebt heel goed opgemerkt dat A vele verschillende gedaantes kan hebben.

Ik heb wel een bruin vermoeden hoe je dit moet aanpakken, en dat vermoeden zal ik je vertellen.
Maar je moet zelf wel even checken of dat vermoeden ook onder alle omstandigheden zal kloppen.

Wanneer je een vector (k,l,m)^T hebt, en die wil je middels matrix A zodanig draaien dat de vector samenvalt met de z-as, dan betekent het feitelijk dat je A opgebouwd kunt denken als het produkt van twee draaiingen.

1. de eerste draaiing zet (k,l,m)^T om in
(k,0,m)^T, en is dus een draaing om de x-as zdd dat de y-component 0 wordt;
2. de tweede draaiing zet (k,0,m)^T om in
(0,0,m)^T en is dus een draaiing om de y-as, zdd de x-component 0 wordt.

noem de draaiingshoek om de x-as a, en die om de y-as b.

Dan geldt dat

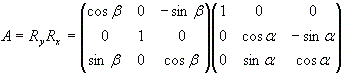
We gebruiken de formule voor de hoek tussen 2 vectoren a en b:
cosq=a·b/|a|.|b|

z=(0,0,1)^T

met cosa= (0,l,m)^T·z/|(0,l,m)^T||z|
= m/(Ö(l²+m²)).1 = m/(Ö(l²+m²))
dus sina= l/(Ö(l²+m²))

We nemen (0,l,m) en niet (k,l,m) omdat we voor de draaiing puur om de x-as, eerst de projectie van (k,l,m) op het OYZ-vlak moeten nemen.

cosb= (k,0,m)^T·z/|(k,0,m)^T||z|
= m/(Ö(k²+m²)).1 = m/(Ö(k²+m²))
dus sinb= k/(Ö(k²+m²))

(k,o,m) is de projectie van (k,l,m) op het OXZ-vlak

A is het produkt van 2 draaiingen dus.

groeten,

martijn

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 6 juni 2003