WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Veeltermfunctie determineren

Hallo,

Ik heb een probleem met een oefening van wiskunde

Bepaal een veeltermfunctie van de 4e graad; die deelbaar is door x-2 & door x+2. Die voor x = -1 de extremawaarde -27 aanneemt en wiens grafiek in het punt met als x-waarde 1 een raaklijn heeft die evenwijdig is met a:2y - 16 x + 3 = 0 (of te wel y = 8x -(3/2))

Ik moet dit determineren, dus schrijf ik eerst de functie op

y: ax⁴ + bx³ + cx² + dx + e
en f'(x) zal er zo uitzien: 4ax³ + 3bx² + 2 cx + d

uit de functie blijkt dat ik 5 onbekenden heb, en dus 5 voorwaarden nodig zal hebben om het dan op te lossen met een matrix.

voorwaarde 1= f'(1) = 8 (RiCo raaklijn)
voorwaarde 2= f(-1) = -27
voorwaarde 3= f'(-1) = 0

En nu is mijn vraag: wat zijn voorwaarde 4 & 5. Ze zullen iets te maken hebben met die deling, maar wat? Hoe giet ik dat in een voorwaarde?

Dieter
3de graad ASO - woensdag 4 juni 2003

Antwoord

Wel. Je doet het betrekkelijk goed. Alleen gebruik je, zoals je zelf zegt, niet het gegeven dat de functie moet deelbaar zijn door x+2 en x-2. De algemene 4degraadsvergelijking die deelbaar is door x+2 en x-2 is:

(x-2)*(x+2)*(a*x²+b*x+c) met a,b,c nader te bepalen constanten.

Na uitrekenen:
x⁴*d+x³*b+x²*c-4*d*x²-4*b*x-4*c

Nu heb je voldoende vergelijkingen om het zelf te kunnen.

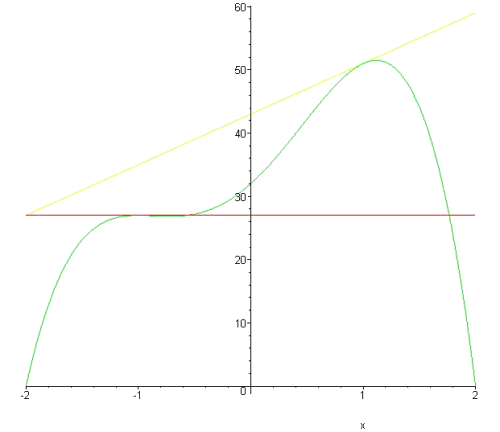
Hier het antwoord en een figuurtje:

-5*x⁴-4*x³+12*x²+16*x+32
of ontbonden: (x-2)*(x+2)*(-5*x²-4*x-8)

figuur:

Koen Mahieu

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 4 juni 2003

Re: Veeltermfunctie determineren