WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Coordinaten tussen een cilinder en een lijn

Ik heb een opgave waarbij gegeven een cilindervlak C: y²+z²=25. De lijn l: (x,y,z)=(5,7,4)+t(0,3,1) snijdt in de punten A en B.
Hierbij moet bepaald worden wat de coordinaten van A en B zijn.

Allereerst heb ik het cilindervlak omgeschreven naar een parametervoorstelling: (x,y,z)=(u,5*cos(v),5*sin(v))

Vervolgens heb ik de lijn en het cilindervlak aan elkaar gelijk gesteld:
| u = 5
| 5*cos(v) = 7 + 3t Û
| 5*sin(v) = 4 + t

| u = 5
| cos(t) = 1 2/5 + 3/5 t
| sin(t) = 4/5 + 1/5 t

Echter op dit punt loop ik vast. Kunt u mij hier verder mee helpen?
Eelco
Leerling bovenbouw havo-vwo - maandag 2 juni 2003

Antwoord

Figuur:

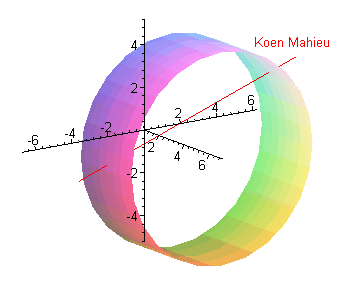
In de tweede stap maak je een foutje door v in t te veranderen. Dat zijn twee verschillende parameters en dat moet zo blijven. Wat je duidelijk ziet is dat u gekend is (5) en bijgevolg is de x-component van de oplossing 5. Die doet dus in de berekeningen al niet meer mee.

We hebben:

cos(v) = 1 2/5 + 3/5 t
sin(v) = 4/5 + 1/5 t

Dit is een stelsel van twee vergelijkingen en twee onbekenden. Het heeft twee verschillende oplossingen. Dit zou je volgens mij zelf moeten kunnen oplossen naar t (en v). Als je de waarden van t hebt vul je die in in de parametervergelijking van de rechte. Dit geeft je de te zoeken y- en z-component.

Hint:
Maak gebruik van de grondformule van de goniometrie om het stelsel te reduceren: sin²(v)+cos²(v)=1. Dus kwadrateer de vergelijkingen en tel ze op. Zo vind je de waarden voor t.

antwoord:
r₁(5,-5,0)
r₂(5,4,3)

Koen Mahieu

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 2 juni 2003

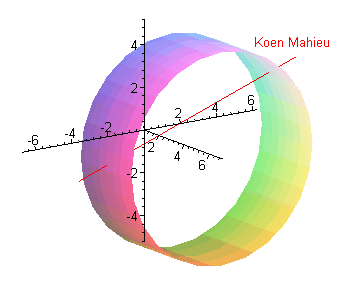
Re: Coordinaten tussen een cilinder en een lijn