|
|
|
\require{AMSmath}



Vliegtuig
Een vliegtuig heeft 4 motoren, 2 motoren aan elke vleugel Elke motor heeft een kans op uitvallen tijdens een vlucht van 10 tot de macht -3. Men noemt Fmotor = 10 tot de macht -3 de faalkans van een motor. De kans 1-Fmotor = 999/1000 noemt men de overlevingskans- of bedrijfszekerheid Rmotor van de motor.
Gevraagd:
1)
bereken de kans op uitvallen van het vliegtuig tijdens een vlucht als:
* 2 motoren aan dezelfde vleugel uitvallen;
* 2 motoren uitvallen(ongeacht de plaats);
* 3 of meer motoren uitvallen.
2)
Hoe zou de formule moeten luiden voor de bedrijfszekerheid Rtotaal van een systeem met n componenten dat blijft leven indien allen n componenten met bedrijfszekerheid R1, R2,....Rn noodzakelijk zijn? M.A.W. er mag niet een component uitvallen.
3)
Hoe zou de formule moeten luiden voor de overlevingskans Rtotal van een systeem dat blijft leven zolang een of meer van de n componenten met de bedrijfszekerheid R1, R2,....Rn nog blijven functioneren? M.A.W. het systeem valt pas uit als alle componenten uitgevallen zijn.
4)
Hoe zou de formule moeten luiden voor de overlevingskans Rtotaal van een systeem dat blijft leven zolang er nog m van de n componenten R1, R2,....Rn blijft functioneren. M.A.W. het systeem vlat uit indien meer dan n-m componenten van de n componenten uitgevallen zijn. Men mag bij de beantwoording van deze laatste vraag er van uit gaan dat alle n componenten dezelfde bedrijfszekerheid bezitten(R1=R2=...=Rn).
Ciao
Dualba
Student hbo - maandag 2 juni 2003
Antwoord
Poe poe...
1.
P(uitval)=0,001
De kans op uitval van twee motoren aan één vleugel is:
0,001·0,001=0,000001
Maar je het 2 vleugels!
Dus: 2·0,000001=0,000002
P(2 motoren)=Comb(4,2)·0,0012·0,9992
P(3 of 4)=Comb(4,3)·0,0013·0,999+0,0014
2.
Is dat niet gewoon R1·R2·R3·...Rn? (zeg maar de kans dat alle componenten blijven werken)
3.
Is dat niet 1-((1-R1)·(1-R2)·(1-R3)·...(1-Rn))? (zeg maar 1 min de kans dat alle componenten uitvallen)
4.
Met n:aantal en m:aantal uitvallers en p=R1 is de kans dat het systeem NIET uitvalt een binomiale stoachast:
Binom(X m;n;p) m;n;p)
Dus:
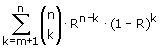 ? ?
Zoals je ziet staan er wel erg veel vraagtekens in dit antwoord. Ik denk dat het wel klopt, maar 't is al laat...
Misschien moet je bij dat laatste antwoord even controleren of het klopt met een voorbeeld...

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 4 juni 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 m;n;p)
m;n;p) 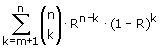 ?
? 

