WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Formule voor de dimensie van een fractaal

Hallo,

Ik moet voor school een aantal vragen beantwoorden over onder andere de dimensie van bepaalde fractals (zoals bijvoorbeeld de Koch-kromme en de Draakkromme). Ik heb hiervoor de formule n=c·k^d, waarin n het aantal kubusjes dat nodig is om de figuur te bedekken voorstelt, k de verkleiningsfactor is en d de dimensie. De c wordt beschreven als een of ander constant getal. Ik weet echter niet hoe deze c te berekenen is. Ik hoop dat u me kunt helpen. Alvast bedankt voor uw antwoord.
Peter
Leerling bovenbouw havo-vwo - vrijdag 30 mei 2003

Antwoord

We hebben de formule:

n=c·k^d

n: aantal 'kubusjes'
c: een of andere constante
k: verkleiningsfactor
d: dimensie

Laten we een voorbeeld nemen:

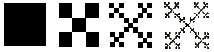
Je ziet hier een 'boxfractal'. Nu ken ik wel een andere formule:

N=S^D

In dit geval is N=5 en S=3, zodat D=log5/log3=1,4649

Dat lijkt veel op jouw formule, maar je omschrijvingen zijn wel vaag! Wat is hier de verkleiningsfactor k? Is k=¹/₃ of is k=3. En hoe bereken jij d? Of wilde je nu juist jouw formule daarvoor gebruiken!? In dat geval kan je beter bovenstaande formule gebruiken.... (volgens mij geldt hier dan c=1)

Kortom: nogal vaag... Kijk maar eens op onderstaande website. Dat maakt het misschien allemaal een stuk duidelijker. Daarna nog vragen dan horen we het wel.
Zie Mathematical Interpretation of Fractal Dimension

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 31 mei 2003