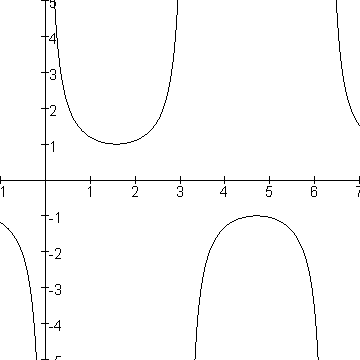WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Het bereik en asymptoten bepalen

Weet iemand hoe men het bereik kan bepalen van deze functie f(x)= 1 + 2 sin x op domein [0.2$\pi$] ?

Ik had ook nog een vraagje over asymptoten berekenen van deze functie g(x)= 1/(sin x) Men moet dan sin x =0 stellen(denk ik ) maar dan krijg je x =0 het antwoorden boek heeft als antwoor x = $\pi$, asymptoten bepalen vind ik sowieso moeilijk zou u misschien een paar tips kunnen geven hoe men makkelijk asymPtoten kan bepalen vooral met dat soort functies dat ik bovenaan heb getypt ?

Bijvoorbaat dank
David
Leerling bovenbouw havo-vwo - woensdag 28 mei 2003

Antwoord

Hoi,

sin(x) is het domein [0;2$\pi$] kleiner dan of gelijk aan 1 en bovendien groter dan of gelijk aan -1,
dus -1$\leq$sin(x)$\leq$1.
dus -2$\leq$2sin(x)$\leq$2
dus -1$\leq$1+2sin(x)$\leq$3.
Het bereik is dus [-1;3].

Voor wat betreft asymptoten bij dit soort functies:
Omdat dit periodieke functies zijn hoef je alleen naar verticale asymptoten te zoeken.
Deze vind je waar de noemer nul is.
Bij f(x)=1/sin(x) is de noemer sin(x).
Je moet dus oplossen: sin(x)=0.
Op het domein [0;2$\pi$] is dit voor x=0, x=$\pi$ en x=2$\pi$.
De asymptoten zijn dus x=0, x=$\pi$ en x=2$\pi$.

Als je de grafiek tekent dan zie je dat ook.

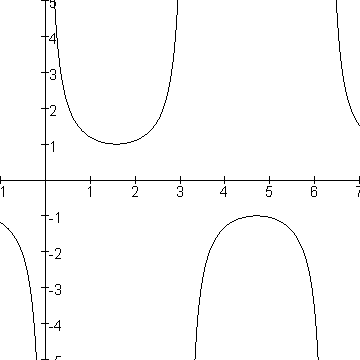
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 28 mei 2003