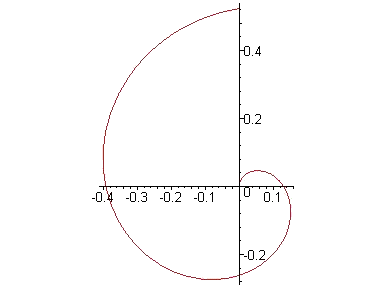WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Booglengte berekenen van een archimedische spiraal

hoe doe ik dit.. ik heb dus de functie
x=(1/3)tsin(4t)
y=(1/3)tcos(4t)
de primitieve van de snelheidsformule zou kunnen maar dat kan niet want dan kom je in de hoop met de productregel ( Ö((1/144)t²+(1/9)) )
moet ik dan helemaal de formule in de vorm van y=ax+b gaan omschrijven of is er ook een andere manier? (formule)

alvast bedankt,

leonardo
leonar
Leerling bovenbouw havo-vwo - maandag 26 mei 2003

Antwoord

Dit kan heel eenvoudig met een lijnintegraal.

Je hebt een parametervoorstelling gegeven van je kromme G:

x=1/3·t·sin(4·t)
y=1/3·t·cos(4·t)

De booglengte is:

$\int{}$_Gds

met ds=√(dx²+dy²) ·dt

dx= ¹/₃ ·(sin(4·t)+4·t·cos(4·t))=1/3·sin(4·t)+4/3·t·cos(4·t)
dy=1/3·cos(4·t)-4/3·t·sin(4·t)

$\Rightarrow$ na het uitwerken (rekening houdend met de grondformule van goniometrie sin²+cos²=1):
ds=√(1/9+16/9·t²) dt
de lijnintegraal wordt:

₀$\int{}$^a√(1/9+16/9·t²) dt

= 1/6·a·√(1+16·a²)+1/24·arcsinh(4·a)

Hierin is a de waarde van de parameter t van de parametervoorstelling G Op de figuur is a=$\pi$/2

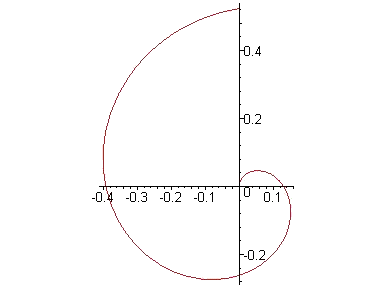
De waarde van de integraal wordt voor a=$\pi$/2:
Booglengte=1/12·Pi·√(4·Pi²+1)+1/24·arcsinh(2·Pi)$\approx$1.771357846

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 26 mei 2003