WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Goniometrie

Hoi wisfaq,
Ik ben met een opgaven bezig over de sinusfunctie, maar ik krijg steeds een heel ander antwoord uit mijn berekening dan wat er in het antwoordenboek staat, ik zal eerst de opgaven plus de antwoorden volgens het antwoorden boek "opschrijven" en toelichten wat ik gedaan heb.

1 a) Voor a= 1/4p+k.2p geldt sin a= 0,707 (ongev.)
Voor welke waarden van a krijg je dezelfde functie waarde ?
b) geef alle oplossingen van sin a= -0,707
c) dezelfe opdracht voor sin a= 0,3

-- Antwoordenboek:
a) a=3/4p+k.2p

b) 5/4p+k.2p of 7/4p+k.2p
(ook: a=-1/4p+k.2p of -3/4p+k.2p

c) a=0,3+k.2p of a=2,8 +k.2p

Nu dacht ik zelf dat men voor k= 1 moest invullen om aan de antwoorden te komen, omdat ik dat deed voor de andere opgaves waarmee ik bezig was, en ik kreeg keurig de antwoorden die ook in het antwoordenboek stonden, maar hier werkt het niet !

Hoe komen ze aan die antw. ? Kunnen jullie me helpen ? Kan iemand mij duidelijk maken hoe ze O.A van 0.3p naar 2.8p "vliegen".

Tim
Leerling bovenbouw havo-vwo - zondag 25 mei 2003

Antwoord

Wat bij dit soort opgaven uitstekend van pas komt, is de "eenheidscirkel". Ik neem voor het gemak even aan dat je dat bekend is.

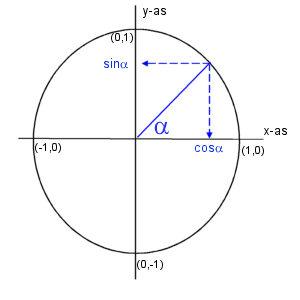
Hierboven zie je zo'n eenheidscirkel.
Je hebt lijn die een of andere hoek a met de x-as maakt. Deze lijn snijdt de eenheidscirkel.
* de x-coordinaat stelt de cosinus voor van a;
* de y-coordinaat stelt de sinus voor van a.

Hierboven hebben we de weg beschreven om (mbv de eenheids-cirkel van een HOEK naar een (CO-)SINUSwaarde te komen.
Nu gaan we het omgekeerde doen:
Stel je hebt de sinus, en je wilt de bijbehorende hoek weten.

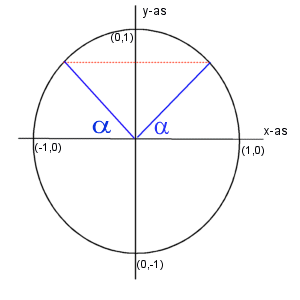
Zoals je aan bovenstaand plaatje kunt zien, kun je uitgaande van één bepaalde sinuswaarde TWEE hoeken erbij vinden die deze sinuswaarde zullen opleveren.
namelijk de hoeken a (mod 2p) ENNNNN p-a (mod 2p)

Ga voor jezelf na (door aan te wijzen op de eenheidscirkel) dat bij een zekere cosinuswaarde, TWEE hoeken horen, te weten a en -a (beiden mod 2p uiteraard)

nu jouw opgaven.
die 0,707 is gewoon even ¹/₂Ö2 omdat dat zo'n "mooie waarde" is in de gonio.
1. sina=¹/₂Ö2
hier horen dus 2 hoeken a bij, die je allebei dezelfde sinus (te weten ¹/₂Ö2) zullen opleveren.
namelijk a=p/4 + 2kp Ú
a= p - p/4 + 2kp, ofwel 3p/4 + 2kp

2. sina=-¹/₂Ö2
Þ a=5p/4 Ú a={p- 5p/4}=-p/4
je eindantwoord zou dus kunnen luiden:
a=5p/4 + 2kp Ú a=-p/4 + 2kp
alleen is het gebruikelijk om alleen positieve hoeken te noemen. Dus we moeten nog even wat sleutelen aan die -p/4. Daar tellen we simpelweg 2p bij op, zodat we op 7p/4 uitkomen, en het antwoord dus luidt:
a=5p/4 + 2kp Ú a=7p/4 + 2kp

3. sina=0,3 Þ
a= .. +2kp Ú a= {p- ..} + 2kp
etc...

groeten,
martijn

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 25 mei 2003