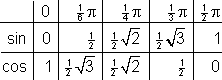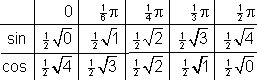WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Goniometrie

Hallo wisfaq,
Ik ben begonnen zelfstandig aan een hst over goniometrie en heb al problemen met de eerste paragraaf er wordt geen uitleg gegeven over de opgaven, kennnelijk gaan ze ervan uit dat men dit nog kent, maar het is al zolang geleden voor mij sinds ik gonio heb gehad, ik hoop dat ik door mijn vragen en uw antwoorden het onderwerp beter begrijp.

-Mijn eerste vraag is hoe kan men van graden naar radialen gaan en dan weer terug b.v als men dit heeft :
2/3p hoeveel graden is dit?

-vraag 2: als ik cos(1/4p) met mijn rekenmachine bereken krijg ik 0.707.. uit maar in het antwoordenboek zetten ze :
0.5Ö2 en tan(1/6p)=-2.835...
Het antwoordenboek zegt 1/3Ö3, nu weet ik dat ze allebei gelijk zijn maar ik wil graag leren hoe ze dit zo "mooi" opschrijven weet u dit misschien ?

-vraag 3: Hoe kan men sin(.5p-2t) uitdrukken in sin(t) ?

Alvast bedankt voor het beantwoorden,
Groet,
Tim

Tim
Iets anders - vrijdag 23 mei 2003

Antwoord

vraag 1:
Een radiaal kun je je het beste voorstellen als de hoek, die je krijgt als je een spaak uit een fietswiel haalt, en deze langs de velg buigt. De spaken die in de velg zitten aan de beide uiteinden vormen bij de as juist een hoek van 1 radiaal.

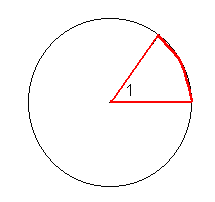
Een hoek van 2 radialen krijg je als je twee spaken langs de velg legt, enzovoort.
Als de spaaklengte 1 is, is de lengte van de boog gelijk aan de hoek in radialen.
Zo hoort bij een hoek van 180° (een gestrekte hoek) een boog die de halve cirkelomtrek lang is, dus p radialen.
Een hoek van 45° is een kwart van de gestrekte hoek, dus ook ¹/₄p radialen.
De algemene formule luidt:
x° = ^x/₁₈₀·p radialen
en andersom:
y radialen = y·(¹⁸⁰/_p)°

vraag 2:
sinus en cosinus kun je heel mooi in de eenheidscirkel aflezen. Voor een aantal 'mooie hoeken' is een standaard berekening gemaakt. In het volgende tabelletje zie je een overzicht van deze berekeningen. Ze zijn allemaal gebaseerd op het toepassen van de stelling van Pythagoras, als dat je nog wat zegt.

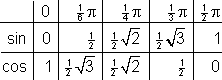
Het volgende tabelletje is een ezelsbruggetje om deze mooie waarden gemakkelijk te onthouden.

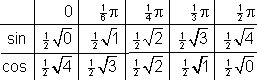
Voor de tangenswaarden moet je de sinuswaarde delen door de cosinuswaarde.

vraag 3:
Er zijn diverse gonioformules. Het voert te ver om deze hier allemaal op te nemen. Ik geef er twee, die hierbij van nut zijn.
sin(¹/₂p-x) = cos(x)
cos(2x) = 1 - 2·sin²(x)
Dus: sin(¹/₂p-2t) = cos(2t) = 1 - 2·sin²(t)

Hierbij moet je de notatie sin²(x) lezen als: het kwadraat van sin(x).
succes!
groet,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 23 mei 2003