|
|
|
\require{AMSmath}



Wat is de sinusfunctie?
Ik ben op zoek naar wat meer uitleg i.v.m. de sinusfunctie. Wat is de sinusfunctie? Hoe kan ik me dit voorstellen? Hoe geraak ik van een sinusfunctie naar een cosinus funtie?
Gaat dit ook voor een tangens?
Wim Ho
Student Hoger Onderwijs België - maandag 30 december 2002
Antwoord

Hoi Wim,
De sinusfunctie is -zoals de naam al zegt- de functie van de sinus. Maar wat is de sinus? De sinus is een goniometrische functie. En goniometrische functies kunnen worden voorgesteld op de goniometrische cirkel (=eenheidscirkel), die cirkel heeft als straal 1.
Waarom straal 1? Wel een cirkel met middelpunt O(0,0) heeft als algemeen voorschrift straal2= x2 + y2, en langs de y-as komt de sinus te staan, en langs de x-as de cosinus dus krijg je als functievoorschrift (sin (x))2 + (cos(x))2 = sin2x + cos2x en dit is uiteraard gelijk aan 1. (Je kunt dit ook bewijzen a.d.h.v. de Stelling van Pythagoras, je krijgt dan als hypotenusa2 = sin2x + cos2x, dus schuine zijde is 1, immers straal van cirkel).
Beschouw nu 'n georiënteerde hoek a, die de cirkel in een bepaald punt snijdt. Noem dit punt A. Projecteer dit punt op de x-as en op de y-as (m.b.v. een horizontale en een verticale lijn, loodrecht op elkaar). Punt A heeft nu het coördinatenpaar (cos a, sin a) omdat de afstand vanaf de oorsprong tot het punt waar de x-as gesneden werd door de "projectie-lijn" = cos a, en de afstand vanaf de oorsprong tot het punt waar de y-as gesneden werd = sin a. Je hebt nu visueel voorgesteld wat sin a en cos a betekenen, want je kunt aflezen van de goniometrische cirkel welke waarde de sinus heeft en welke waarde de cosinus heeft.
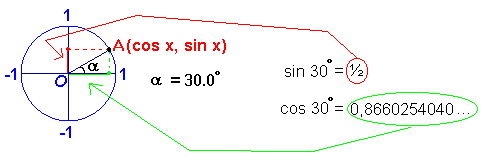
Hier beschouwen we de georiënteerde hoek a = 30°.
Punt A is eigenlijk (cos a, sin a) (dus niet x), dus hier toegepast A(cos 30°, sin 30°), aflezen op cirkel geeft sin 30° = 1/2, en cos 30°  0,9 (exacte berekening uiteraard via rekenmachine). 0,9 (exacte berekening uiteraard via rekenmachine).
De verschillende hoeken van a liggen tussen 0° en 360° en de bijbehorende waarden liggen altijd tussen -1 en 1.
We kunnen de waardes van sinus en cosinus ook in een grafiekje zetten. Maar omdat we de gon. cirkel zo vaak kunnen doorlopen als we willen krijgen we steeds dezelfde waarden te zien, m.a.w. de functies zijn periodiek er onstaan 'golfbewegingen', daarom worden de sin en cos-functie ookwel sinusoïden genoemd.
De sinusfunctie (op de gon. cirkel de y-as) gaat vanaf de oorsprong gezien, van 0 (sin 0° = 0) naar 't maximum 1 (sin 90° = 1) dan weer naar 0 (sin 180° = 0) en vervolgens naar het minimum -1 (sin 270° = -1) om vervolgens weer naar de beginpositie 0 te gaan (sin 360° = sin 0° = 0). Deze beweging herhaalt zich telkens, zie onderstaande grafieken.
De cosinusfunctie is 1 als a = 0°. Indien a = 90° is cosinus = 0. cos 180° = -1, cos 270° = 0 en vervolgens de beginpositie cos 360° = cos 0° = 1. De cosinus heeft blijkbaar hetzelfde verloop als de sinus, alleen is er een verschuiving. Hieronder zie je de sinus én cosinusfunctie in een plaatje getekend.
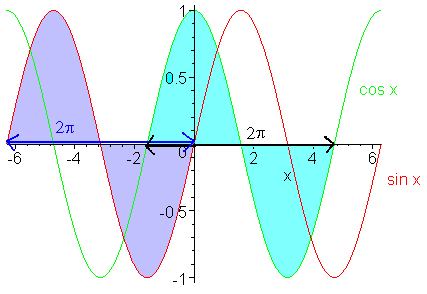
Er is telkens de golfbeweging te zien, het gedeelte boven de x-as is even groot als het gedeelte onder de x-as (zie gearceerd gedeelte), deze gedeeltes komen telkens terug en bestrijken een lengte van 2p. Blijkbaar is de goniometrische cirkel helemaal doorlopen, na 2p (hetgeen overeenkomt met de omtrek, want straal = 1, dus diameter = 2, en omtrek cirkel = p´d = 2p). Een cirkel heeft 360°, dus 2p = 360°. Indien je nu direct van graden naar getallen (=radialen) wilt gaan, kun je de volgende formule gebruiken (aantal graden ´ p) / 180°. Andersom (van rad Þ grad) = (aantal radialen ´ 180°) / p.
De tangensfunctie construeren vanuit de eenheidscirkel is iets moeilijker, klik op 3. Tangens-functie om hierover meer informatie te krijgen.
Dan hoe je de sinus kunt schrijven in functie van de cosinus en omgekeerd. In bovenstaande grafiek heb ik de twee functies in één plaatje geplot, nu kun je afleiden uit de grafiek dat de sinusoïden p/2 van elkaar verwijderd liggen (=faseverschil). Dus cos x = sin(p/2 - x) en sin x = cos(p/2 - x).
De tangens kun je schrijven als tan x = sin x / cos x.
Groetjes,

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 30 december 2002
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|









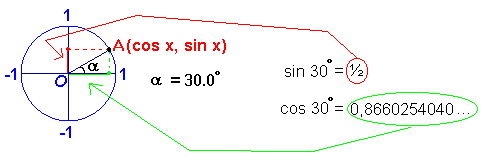
 0,9 (exacte berekening uiteraard via rekenmachine).
0,9 (exacte berekening uiteraard via rekenmachine).


 Re: Wat is de sinusfunctie?
Re: Wat is de sinusfunctie?