WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Staartdeling toepassen bij limieten

Hallo wisfaq,

Ik weet niet precies waarom ik de volgende opgaven fout doe, misschien weten jullie het.

Gegeven: f(x)= I x³-1 I / (x-1)

Gevr.a) bereken linker limiet x gaat naar 1 van f(x)
En de rechter limiet x gaat naar 1

B) teken de grafiek

Dan ga ik als volgt te werk ;

X $>$ 0 f(x)= (x³-1)/(x-1) -$\to$ (na staartdeling) x²+x+1

Maar voor X $<$ 0 f(X)= (-x³+1)/(x-1)schijn ik een fout te maken maar wat ?

Staartdeling : x-1 /-x³+1\ -x²+x+1
-x³+x²
-----
x²+1
x²-x
----
x+1
x-1
---
2

Dus f(x) voor x$<$0 is -x²+x+1 + (2/x-1)

Nu zijn mijn vragen waarom is dit fout ? En hoe moet men de grafiek dan tekenen ? door gewoon een tabel maken met x waardes met de bijbehorende y waardes voor X $>$ 0 en voor X $<$ 0 of doet men dit anders ?

Als iemand dit sommetje kan uitleggen dan graag.

Tim
Leerling bovenbouw havo-vwo - woensdag 14 mei 2003

Antwoord

Als ik het goed begrijp is de functie f gegeven door f(x)=|x³-1|/(x-1).
Je splitst de functie niet juist, want er geldt:
|x³-1| = x³-1 als x³-1$>$0, dus als x$>$1, en
|x³-1| -x³+1 als x$<$1.
Jouw eerste staartdeling is OK, maar in de tweede maak je fouten met de min-tekens. Kijk maar:
Staartdeling: x-1 /-x³+1\ -x²-x-1
-x³+x²
-----
-x²+1
-x²+x
----
-x+1
-x+1
---
0
Dat had je ook tevoren kunnen bedenken, als x$<$1 is er in de teller een min-teken bij gekomen.
De linker- en rechterlimiet van f(x) als x nadert naar 1 zijn niet gelijk aan elkaar:

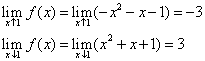
Je moet nu twee parabolen tekenen, tabellen maken (rondom de top) zal wel volstaan. De linker (berg)parabool eindigt bij punt (1,-3), en de rechter (dal)parabool gaat dan na een sprong verder na punt (1,3).
In x=1 is de functie niet gedefinieerd dus de twee eindpunten moet je in de grafiek voorzien van open rondjes.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 14 mei 2003

Re: Staartdeling toepassen bij limieten