WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Parabolen: vergelijkingen en raaklijnen

Dit is een reactie op vraag 10742

Bedankt voor je snelle reactie Anneke. Ik zal het verhaal van vraag 1 eens rustig bestuderen.
Mbt vraag 2, gegeven is y=2cx². Voor elke parabool geldt: y=(1/4c)x². Dan geldt: 2c=1/4c, maw 2c*4c=1, 8c²=1, c²=1/8, c=+/- wortel 1/8 = wortel(2)/4.

mvg, Lisanne
Lisann
Student hbo - vrijdag 9 mei 2003

Antwoord

Ik denk dat er hier een misverstand is vanwege het dubbele gebruik van de letter c. Ik neem aan dat in de opgave voor c een willekeurige constante bedoeld wordt, en niet de coordinaat van het brandpunt.
Maar goed, los daarvan is het antwoord op de vraag ook te geven.
Ik neem aan dat je weet dat de poollijn van een punt op de richtlijn door het brandpunt (noem dit F) gaat.
Neem nu een punt P op de richtlijn. De poollijn van P snijdt de parabool in de twee raakpunten C en D.
Noem A het voetpunt van de loodlijn uit D op de richtlijn, en B het voetpunt van de loodlijn uit C op de richtlijn.

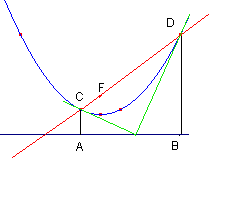
Bekijk nu het rechthoekig trapezium ABCD. De raaklijn PD is de bissectrice van hoek ADC (vanwege de definitie van een parabool), en de raaklijn PC is de bissectrice van hoek BCD.
Je kunt nu eenvoudig aantonen dat hoek CPD gelijk is aan 180° minus de helft van (hoek ADC + hoek BCD), dus 90°

groet, Anneke

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 9 mei 2003