WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Zonnestand en daglengte

Beste wiskundigen,
Ik wilde graag weten hoe je de zonshoogte op een ander tijdstip moet bereken met een formule. Ik moet voor ANW de zonshoogte meten en drie weken later nog een keer. Maar ik wilde het graag met een formule controleren. Ik wil dus een formule waarmee ik met de zonshoogte in graden van vandaag, de zonshoogte van drie weken later ook kan berekenen.

Anonie
Leerling bovenbouw havo-vwo - donderdag 8 mei 2003

Antwoord

Een echte formule kun je wellicht zelf afleiden. Laten we even kijken wat er gebeurt. Wij zitten op 52,5° noorderbreedte (wordt aangegeven met het pijltje uit de cirkel). Op 21 december staat de zon loodrecht boven 23,5° zuiderbreedte, op 21 juni loodrecht boven 23,5° noorderbreedte. Als je aanneemt dat de zon gelijkmatig verschuift (in een half jaar heen en daarna weer terug) kan je op elke dag berekenen waar de zon dan staat.
Voor 21 december heb ik dat in het onderstaande eerste plaatje gedaan. Het tweede plaatje geeft de situatie op 21 juni weer. Je ziet de respectievelijke invalshoeken van de zonnestralen op het midden van de dag van 14° (21 dec) en 61° (21 juni). Ook dit verloopt bij benadering gelijkmatig in een half jaar. Nb de vertikale en horizontale zwarte stippellijnen staan loodrecht op elkaar.

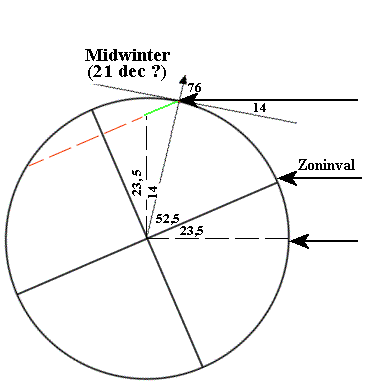
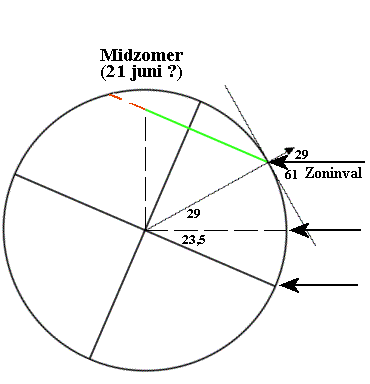
Maar er kan nog meer: de lengte van een dag berekenen op bijvoorbeeld 21 december. De aarde draait om haar as. Op 52,5° nbr wordt een cirkel afgesneden waarvan de middellijn (rood/groen) getekend is. Het groene t.o.v. het rode gedeelte geeft de verhouding licht/donker weer: op 21 december is het grootste gedeelte van de afgesneden cirkel in duisternis gehuld, dat betekent dat het op die dag veel langer donker is dan licht.
Hoelang? dat valt uit te rekenen.
Met de tangens (onderstaand plaatje links) kun je de verhoudingen van het rode en groene deel berekenen. Het rode deel is (0,4348/0,7673)ste deel van de cirkelstraal = 0,5666^e deel. (ps. de hoek van 22,5° in de tekening moet natuurlijk zijn 23,5°)
Welk deel van de cirkel zit nu in het licht. Aangezien het om een verhouding gaat mag je dat met de eenheidscirkel berekenen. Het gaat nu om de cirkelhoek waar het gebied met licht bij hoort. Van de halve cirkelhoek is de cosinus = 0,5666 (onderstaand plaatje rechts).

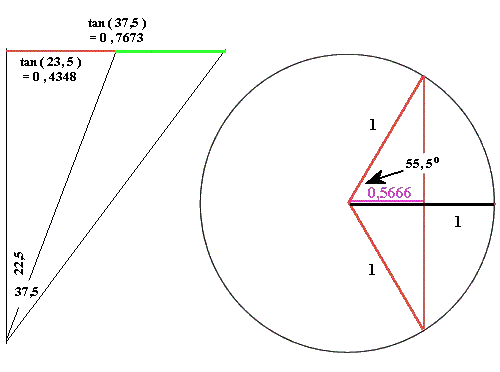
Dan is de halve hoek 55,5°. De totale hoek is 111° en de lengte van de dag op 21 december wordt nu 111/360·24uur = 7,4 uur.
En op 21 juni ? Ik denk dat we dan erbij krijgen wat er op 21 december afgaat. 12+4,6=16,6 uur. Ofwel dan is het 7,4 uur donker. Met behulp van berekening van een paar extra hoekjes in de eerste twee cirkels is dat makkelijk aan te tonen.

Met vriendelijke groet

JaDeX

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 10 mei 2003