WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Bewijs formule Ptolemeus

Hoi!

Ik heb een vraag: zouden jullie mij uit kunnen leggen hoe ik de formule van Ptolemeus kan bewijzen?
De formule is:
AB x CD + AD x BC = AC x BD. De formule hoort bij een koordenhoek in een cirkel, maar ik heb nog niks over koorden gehad, dus als het zonder koorden kan en alleen met sinussen en cosinussen en zo, zou dat heel fijn zijn!
Ik heb veel geprobeerd maar ik kom er niet uit!
Alvast bedankt!
Esther
Leerling bovenbouw havo-vwo - dinsdag 29 april 2003

Antwoord

dag Esther,

Het is niet zo gek dat je er niet zomaar uitkomt, want het is best ingewikkeld.
Eerst een hulpstelling: de stelling van Stewart.
Dit passen we toe in onze koordenvierhoek:

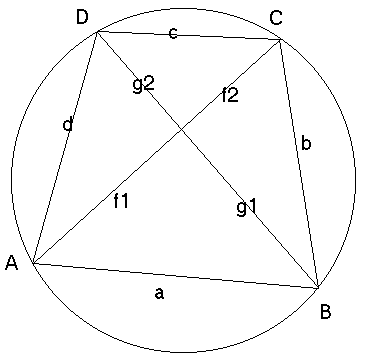
f₁²g=d²g₁+a²g₂-g₁g₂g

Nu is DASD~DBSC (gelijkvormig omdat de hoeken gelijk zijn)
Hieruit volgt: f₁:d=g₁:b, dus f₁b=g₁d
en ook: f₁:g₂=g₁:f₂, dus f₁f₂b=g₁g₂
Verder is DASB~DDSC
Hieruit volgt: f₁:a=g₂:c, dus f₁c=g₂a

Als we dit invullen in de toepassing van Stewart, krijgen we:
f₁²g=bdf₁+acf₁-f₁f₂g, dus f₁g=ac+bd-f₂g
en hier staat de stelling van Ptolemeus!

groet, Anneke

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 30 april 2003