WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

vlakke meetkunde

Gegeven is een driehoek ABC met oppervlakte S=1. Op de rechten CA, AB, en BC worden punten A',B' en C' bepaald door volgende (Vectoriële) gelijkheden ; AA'=kCA
BB'=lAB (k,l,m 1)
CC'=mBC
Gevraagd wordt de oppervlakte S' van de driehoek A'B'C' uit te drukken als functie van enkel k,l en m .

Ze geven hierbij volgende redenering;

S(AB'C) = (1+l)S(ABC) zodat S(AA'B)=kS(AB'C)=k(1+l) en zo analoog te redeneren voor driehoeken BB'C en CC'A .
Ik snap niet hoe je aan die verhoudingen komt al van in het begin, welke redenering zit er achter dat die ene (1+l) keer de andere driehoek is en dan dat de oppervlakte van AA'B k keer de oppervlakte van AB'C is ????? Hoe beredeneer of hoe zie je dat ????
Berten
3de graad ASO - zaterdag 19 april 2003

Antwoord

De 'truuk' komt neer op het vergelijken van de bases van twee driehoeken die dezelfde hoogte hebben. Hun oppervlaktes zullen zich dan verhouden zoals hun bases.

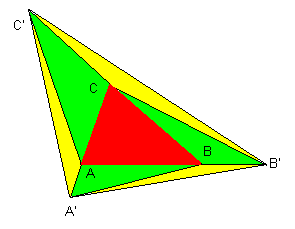
De groene driehoeken hebben een basis die "x" keer langer is dan die van de rode driehoek maar de overeenstemmende hoogtelijnen zijn *gelijk* aan de corresponderende hoogtelijnen in de rode driehoek. Zo wordt:

S(AA'B) = k S(ABC)
S(BB'C) = l S(ABC)
S(CC'A) = m S(ABC)

Op dezelfde manier vergelijken we nu de gele driehoeken met de groene driehoeken

S(AA'C') = k S(CC'A) = km S(ABC)
S(BB'A') = l S(AA'B) = kl S(ABC)
S(CC'B') = m S(BB'C) = lm S(ABC)

Tenslotte is

S(A'B'C')
= S(rood) + S(groen) + S(geel)
= [1 + k+l+m + kl+km+lm] S(ABC)

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 19 april 2003