|
|
|
\require{AMSmath}
Bewijs voor de kwadratuur van de rechthoek
Beste WisFaq,
We hebben een vraag over kwadratuur. Deze luidt: Hoe kun je bewijzen dat de oppervlakte van de kwadratuur van een rechthoek gelijk is aan de rechthoek zelf? De vorming van deze kwadratuur begrijpen we wel. Alleen hoe komt het dat dit ook echt een kwadratuur is?
Bij voorbaat dank,
B, P & M
paul
Leerling bovenbouw havo-vwo - vrijdag 18 april 2003
Antwoord
Ik begrijp niet goed hoe je WEL de constructie kan vinden, maar NIET snapt waarom de oppervlakten gelijk zijn.
Noem de afmetingen van de rechthoek a en b. De zijde van het vierkant moet dan gelijk zijn aan √(ab) en construeer je volgens onderstaande figuur:
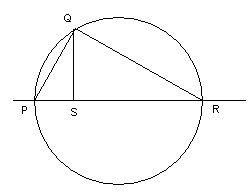
|PS| = a
|SR| = b
De hoek PQR is recht, aangezien hij op een halve cirkel staat. De driehoeken PQS en QRS zijn gelijkvormig zodat
|PS|/|SQ| = |SQ|/|SR| of a/x = x/b of x=√(ab)
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 18 april 2003
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
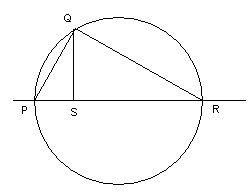
Re: Bewijs voor de kwadratuur van de rechthoek