WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Waarom is de wortel een functie?

Ik dacht altijd dat Öx=a als a²=x. Dit is echter niet volledig. Volgens deze definitie zou Ö9=a namelijk de oplossingen a=3 EN a=-3 (!) hebben (want (-3)²=9). Maar Ö9¹-3. De definitie van de wortel heeft dus een extra beperking namelijk: Öx=a als a²=x en a0. Deze extra regel maakt dat de wortel een functie is, namelijk nu heeft Öx maximaal één beeld "x, en nooit meer dan één wat zonder de beperking wel 't geval kon zijn.

Ik neem aan dat de reden voor die beperking is dat de wortel nu een functie is geworden.

Mijn vraag is nu: Als dit inderdaad de reden is, wat is dan het voordeel van het feit dat t een functie is (wat is t voordeel van functies in t algemeen)?
Als dit niet de reden is, waarom moet de uitkomst van de wortel dán altijd 0 zijn?
Casper
Student universiteit - vrijdag 18 april 2003

Antwoord

In plaats van wortel spreken we ook wel van vierkantswortel. Wat is een vierkantswortel? Je ziet hier onder een aantal vierkanten met verschillende oppervlakten:

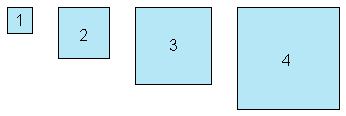
De vraag is wat is de lengte van de zijde?
Bij de eerste en de laatste gaat het nog, maar wat de zijde van een vierkant met oppervlakte 2? Dat is niet zo eenvoudig....
Is het 1,4142135623730950488016887242097?
Nee toch niet (zet ze maar onder elkaar...!)
Want 1,4142135623730950488016887242097² is niet gelijk aan 2. Dan toch liever Ö2?
Dat is beter, want (Ö2)²=2
Kortom: Öx is de lengte van de zijde van een vierkant met oppervlakte x. Je begrijpt dat het geen zin heeft te praten over een vierkant met een zijde van -2 omdat dan de oppervlakte (-2)²=4 is??

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 18 april 2003