WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Van cirkelschijf tot kegel

hoi, ik heb een probleempje waar ik niet uitkom, namelijk;
bereken de overlappingshoek F van een cirkelschijf, met straal 10, waarvan de inhoud maximaal is.
Ik moet hierbij de formule voor de inhoud (I) van de kegel bepalen, waarbij ik I alleen uitdruk in de straal r van de grondcirkel.
alvast bedankt
jasper
Leerling bovenbouw havo-vwo - donderdag 17 april 2003

Antwoord

Wat je precies bedoelt met overlappingshoek begrijp ik niet helemaal, maar misschien is dit wel wat je min of meer zoekt:

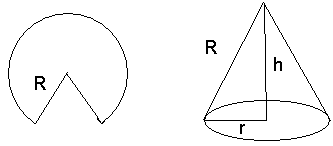
Neem een schijf met straal R en snij er een spie uit zodat je een stuk overhoudt van een hoek a. Daarmee kan je dus een kegel maken met straal van het grondvlak r, hoogte h en apothema R.

De verbanden tussen deze grootheden zijn nu (zie figuur)

2pr = aR Þ a=2pr/R
h = Ö(R²-r²)

Stop die laatste in de formule voor de inhoud van een kegel, en bepaal het maximum (in functie van r). Reken eventueel om naar de hoek a met behulp van de eerste formule.

Je bekomt a = 293.9387692 graden.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 17 april 2003