WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Oppervlakte van de doorsnede

Opdracht en vraagstelling:

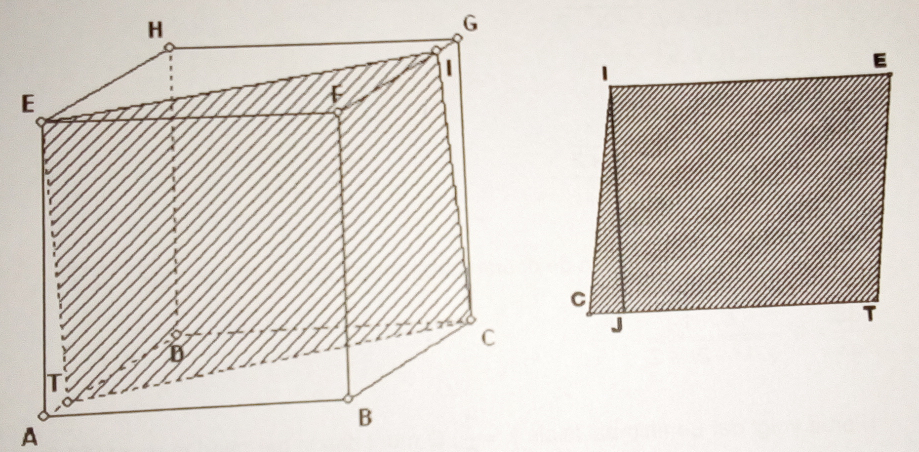
Beschouw een kubus waarvan alle ribben dezelfde lengte a hebben. Op de ribbe AD vinden we het punt T tussen A en D, zodanig dat ^AT/_AD= 1/4.Bereken de oppervlakte van de doorsnedeveelhoek.

Werkwijze:

Ik ben tot de conclusie gekomen dat de doorsnedeveelhoek een parallellogram is.
De oppervlakte daarvan bekom ik door de lengte van CT te vermenigvuldigen met de lengte van IJ.

CT kon ik eenvoudig berekenen want DCT is een rechthoekige driehoek en ik pas de stelling van Pythagoras toe. Zo bekom ik voor CT ^5a/₄.

Ik kom echter in de problemen bij het berekenen van IJ.
De lengte van IC kan ik ook berekenen door dezelfde stelling van Pythagoras toe te passen. Dat geeft me ^{a $\sqrt{}$ 17}/₄.
Maar nu raak ik in de problemen. Ik weet niet hoe ik de lengte van CJ moet berekenen, om zo IJ te bekomen.

Kunt u mij helpen, aub?
Arthur
3de graad ASO - woensdag 20 november 2024

Antwoord

Ik kan het met een beetje valsspelen: je moet in feite het lijnstuk $CI$ loodrecht op $CT$ projecteren om $CJ$ te krijgen. Dat kun je met behulp van vectoren doen: $CI=(\frac14a,0,a)$ en $CT=(\frac34a,a,0)$ (vanuit $C$ liggen $B$, $D$, en $G$ in de positieve $x$-, $y$-, en $z$-richting). De lengte van $CJ$ is dan het inwendig product van de twee vectoren, $\frac3{16}a^2$, gedeeld door de lengte van $CT$ en die is $\frac54a$.

Alternatief: neem $J$ variabel op de lijn $CT$, zeg $CJ=\lambda\cdot(\frac34a,a,0)$. Dan kun je $IJ$ ook in $\lambda$ uitdrukken.
Bepaal dan $\lambda$ zó dat $CJ^2+JI^2=CI^2$; dan is de hoek bij $J$ recht (omgekeerde stelling van Pythagoras).

kphart

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 22 november 2024

Re: Oppervlakte van de doorsnede