|
|
|
\require{AMSmath}



Re: Re: Constructie vijfhoek en bereken max vijfhoek
Dag Klaas -Pieter,
Dit laatste begrijp ik en vond ik ook terug via de stelling van Pythagoras.
Is het nu de bedoeling onderzoek te doen naar de functie die een som moet voorstellen van de oppervlakte van de rechthoek en van de gelijkzijdige driehoek.
Die functie zou er dan, volgens mij zo uitzien
F(x)= (x.(√(900-x2/4)-x√3/2))+x2√3/4
F(x)= (x/2)√(3600-x2-x2√3/2+x2√3/4
F(x)= 1/4(2x√(3600-x2)- x2√3))
Onderzoek van deze functie via afgeleiden en maxima zoeken die ik dan zou moeten toetsen aan de oppervlakte van de vijfhoek. Ik begrijp hier niet goed waar men naartoe wil....
Nog een goede avond.
Rik Le
Iets anders - dinsdag 28 februari 2017
Antwoord
Beste Rik,
Die functie klopt.
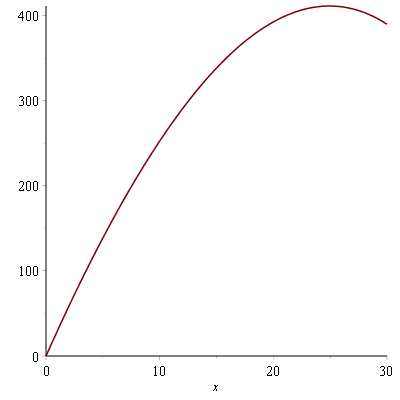
Ik heb maple de grafiek laten plotten:
De afgeleide is
$$
-\frac12\,\frac { \sqrt{3}x \sqrt{-{x}^{2}+3600}+2\,{x}^{2}-3600}{\sqrt{3600-{x}^{2}}}
$$ Als je die gelijk aan nul stelt komt er een vierdegraadsvergelijking die eigenlijk een tweedegraadsvergelijking met $x^2$ er in is:
$$
7x^4-7\cdot3600x^2+3600^2=0
$$ met oplossing
$$
\frac{30}7\sqrt{98-14\sqrt{21}}
$$ De resulterende oppervlakte is
$$
450(\sqrt7-\sqrt3)
$$ Ik zie hier niet veel meer in dan een getruukte differentieersom.
kphart
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 1 maart 2017
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 Dit is een reactie op vraag 83941
Dit is een reactie op vraag 83941 
