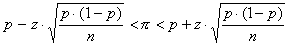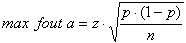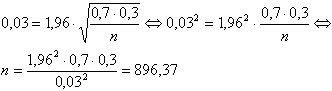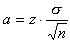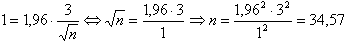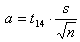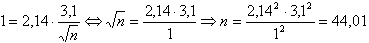WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Steekproefomvang (verschil bij gemiddelden en fracties)

Een onderzoek heeft tot doel het tv kijkgedrag te analyseren. De belangrijkste items zijn:
het percentage mensen dat een ktv bezit
het gem. aantal uren per week dat men tv kijkt
Men wil een aselecte steekpref trekken en met een betrouwbaarheid van 95% wil men een uitspraak doen over beide aspecten.

Als marge hanteert men resp. 3% en 1 uur.
Een vorig onderzoek toonde aan dat 70% een ktv bezit en dat de gem. kijkduur per week 20 uur bedraagt, met een standaarddeviatie van 3 uur.

Wat is de benodigde steekproefomvang??
Pascal
Student hbo - maandag 29 december 2003

Antwoord

Het berekenen van steekproefomvang gebeurt doorgaans om er zeker van te zijn dat je na je onderzoek een bepaalde grootheid kunt schatten met een van te voren vastgestelde maximale fout a. Voordat je deze steekproefgrootte (lees respons) kunt vaststellen moet je je eerst afvragen wat er geschat dient te worden.

In feite kan je ofwel een werkelijk percentage ofwel een werkelijk gemiddelde proberen te schatten.
1a. Benodigde respons bij het schatten van een percentage waarbij niets bekend is:
Weet je helemaal niets van het te schatten percentage dan moet je de basis formule gebruiken zoals beschreven staat in situatie 1 bij Fractieschattingen en respons
1b. Benodigde respons bij het schatten van een percentage waarbij een proefschatting bekend is:
Je wil het percentage bezitters van een KTV schatten. Dit is inderdaad een schatting van een percentage. Soms weet je al ongeveer wat dit percentage moet zijn, dat kan uit een eerder onderzoek (waarbij je aanneemt dat het percentage niet al te zeer veranderd is) of door middel van een vooronderzoek. In jouw geval weet je dat het percentage KTV bezitters ongeveer in de buurt ligt van 70%.

Je wil een schatting voor een werkelijk percentage geven met 95% betrouwbaarheid en een maximale fout in de schatting van 3%. Bij een schatting voor percentages is de formule voor het betrouwbaarheidsinterval:

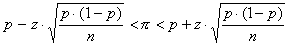
p stelt het werkelijke percentage in de populatie voor, p is de proefschatting (in jouw geval 70% ofwel 0,70). Het verschil tussen p en p is de fout in de percentage uit de steekproef. En van die fout in de schatting wil je dat die in dit geval maximaal 3% is. Dan kun je de benodigde steekproefgrootte berekenen met de formule:

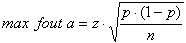
Je kunt nu de formule invullen met fracties 0,03 voor de maximale fout en 0,70 voor de bekende puntschatting. De z waarde van 1,96 komt uit de 95% betrouwbaarheid. Nu kun je de benodigde steekproefgrootte n als volgt berekenen:

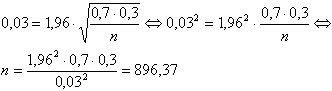
Naar boven afronden levert een benodigde responsomvang van 837 op.
2. Benodigde respons bij de schatting van een werkelijk gemiddelde.
Ook hier bestaan twee varianten van namelijk: je kent de standaarddeviatie van de te schatten variabele (in jouw geval) of je kent de standaarddeviatie niet (gebruikelijk).
2a. Standaarddeviatie bekend:
De formule voor de marge van een betrouwbaarheidsinterval voor gemiddelden is:

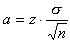
In dit geval weet je dat die waarde van a=1 moet zijn (je wil het werkelijk gemiddelde schatten met een maximale fout van 1 uur). s is gegeven (=3) en die 20 is overbodig.

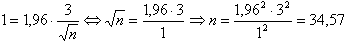
Een respons van 35 is hiervoor voldoende.
2b. Standaarddeviatie onbekend
Stel nu eens dat die standdaarddeviatie niet bekend zou zijn, wat dan?
Je hebt dan een serieus probleem want (kijk naar de formule): zonder standaarddeviatie geen bepaling van de benodigde grootte van de respons.

Je kunt daar op de volgende manier uitkomen. Kies een aantal personen die je als vooronderzoek wil ondervragen, bijvoorbeeld 15 personen. In deze steekproef van 15 personen bereken je uit de genoemde aantallen uren de steekproefstandaarddeviatie s. Neem even aan dat deze 3,1 blijkt te zijn. Omdat je met een geschatte standaarddeviatie werkt, moet je vervolgens een students t-waarde (met 14 vrijheidsgraden) gebruiken in plaats van de z-waarde. Het aantal vrijheidsgraden is dan altijd het aantal ondervraagden - 1.

De formule voor de marge van het betrouwbaarheidsinterval voor gemiddelden is nu:

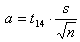
Invullen wat je weet (t₁₄ opzoeken in de tabel van de students t verdeling): levert op.

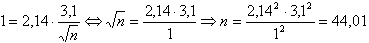
Zodat een totale respons van 45 voldoet. Aangezien je al 15 mensen ondervraagd had, heb je er dus nog 30 extra nodig.

De rest kun je wellicht zelf verzinnen.

Met vriendelijke groet

JaDeX

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 30 december 2003