Hoe begin ik aan een bewijs (in de vlakke meetkunde)?
Hallo!
Ik heb wiskunde B2 en daarbij moet je dingen bewijzen, maar het punt is ik heb geen idee waar ik moet beginnen. Bovendien zie ik daardoor ook niet hoe je het moet bewijzen. Ik hoop dat jullie me kunnen helpen, bijvoorbeeld met een stappenplan of zo iets. Zodat duidelijk is waar ik precies wanneer op moet letten.
Bedankt
Lizett
Leerling bovenbouw havo-vwo - donderdag 24 juni 2004
Antwoord
Ik weet niet welk boek jullie gebruiken, maar in Moderne Wiskunde VWO B2 deel 1 wordt het volgende stappenplan voor de aanpak van een bewijs gegeven:- Verkennen: Maak een analysefiguur waarin alle gegevens zijn aangegeven
- Analyseren Het analyseren bestaat uit drie onderdelen:
- Vooruitdenken: Probeer uit de gegevens het een en ander af te leiden.
- Terugdenken: Bedenk uit hetgene dat bewezen moet worden wat de voorafgaande stap kan zijn geweest.
- Plan maken: Probeer een verband te leggen tussen de resultaten van het vooruitdenken en het terugdenken.
Dit is vaak het moeilijkste deel.
- Bewijs geven
Noteer het bewijs volgens het bewijsschema:- Gegeven
- te Bewijzen
- Bewijs
Op bladzijde 23 en 29 van dit boek wordt dit schema helemaal voorgedaan.
Het voorbeeld van bladzijde 29 komt er kort gezegd op neer:
Stel je weet dat een ruit een parallellogram is met 4 gelijke zijden. Bewijs dan dat daaruit volgt dat de diagonalen van een ruit loodrecht op elkaar staan.
1)Tekening maken en de vier gelijke zijden aangeven.
Schrijf de letter A,B,C en D bij de hoekpunten. Trek de diagonalen en noem het snijpunt S.
resultaat: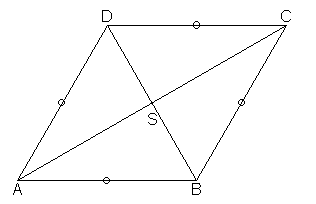
·Vooruitdenken:
ABCD is een parallellogram dus de diagonalen delen elkaar middendoor, dus AS=SC en BS=SD.
·Terugdenken:
Je moet bewijzen dat AC$\bot$BD. Hieruit kun je dus de conclusie trekken dat je kunt volstaan aan te tonen dat $\angle$BSC=$\angle$DSC want $\angle$BSD is een gestrekte hoek.
·Plan maken:
Als ik kan aantonen dat $\Delta$BSC congruent is met $\Delta$DSC ben ik klaar.
Schrijf nu op:
Gegeven: Parallellogram ABCD, AB=BC=CD=DA.
De diagonalen snijden elkaar in S.
te Bewijzen: AC$\bot$BD.
Bewijs:
En nu jij!

vrijdag 25 juni 2004
|
 ©2004-2024 WisFaq
©2004-2024 WisFaq
|