De coördinaten van de top berekenen
Er moet een formule bestaan voor de coördinaten van de top van een parabool. Ik weet wel hoe je de x-coördinaat van de top berekent, maar ik wil ook graag weten hoe je beide coördinaten van de top kan berekenen met een formule?
Bij voorbaat dank.
wilco
Leerling bovenbouw havo-vwo - vrijdag 8 maart 2002
Antwoord
De coördinaten van de top van een parabool kan je herkennen aan de formule als je de formule schrijft in deze vorm:
f(x)=a·(x-p)2+q
De top van deze parabool is (p,q).
Voorbeeld:
Wat is de top van y=(x-2)2-4?
De top is (2,-4)
Voorbeeld:
Wat is de top van y=6·(x+4)2+11?
De top is (-4,11)
Tot zover geen probleem, neem ik aan. Maar ja meestal wordt het functievoorschrift van een parabool gegeven in deze vorm:
f(x)=ax2 + bx + c
Wat je dan kan doen is proberen de formule om te schrijven. Dit kan m.b.v. van kwadraatafsplitsen.
Voorbeeld:
Wat is de top van y=x2-4x+9?
y=x2-4x+9=(x-2)2-4+9=(x-2)2+5
De top is (2,5)
Voorbeeld:
Wat is de top van y=x2+3x-12?
y=x2+3x-12=(x+11/2)2-21/4-12=(x+11/2)2-141/4
De top is (-11/2,-141/4)
Dat was al iets moeilijker. Tot nu toe was a steeds gelijk aan 1, maar dat hoeft natuurlijk niet.
Voorbeeld:
Wat is de top van y=2x2+8x+14?
y=2x2+8x+14=2·(x2+4x)+14=2·((x+2)2-4)+14=2(x+2)2-8+14=2(x+2)2+6
De top is (-2,6)
Nou ja.. zo zou je nog uren door kunnen gaan. De vraag is of dit 'handig' is. Met behulp van de abc-formule is namelijk makkelijk in te zien dat:
Voor f(x)=ax2+bx+c:
xtop=-b/2a
ytop=axtop2+bxtop+c
Volgens mij gaat dat een stuk sneller. Je kan ook kijken naar de afgeleide. Bij de top is immers de afgeleide nul:
f(x)=ax2+bx+c
f '(x)=2ax+b
Wanneer is f '(x)=0?
Als 2ax+b=0
Dus als x=-b/2a
(o, nee dat wisten we al...)
Het is zelfs mogelijk (sommige mensen doen dat) het hele zaakje om te draaien!
Voorbeeld:
Schrijf f(x)=3x2-24x+121 in de vorm f(x)=a(x-p)2+q
xtop=24/6=4
ytop=3·42-24·4+121=73
Dus f(x)=3(x-4)2+73
Conclusie
Voor het berekenen van de coördinaten van de top van f(x)=ax2+bx+c gebruik je:
xtop=-b/2a
ytop=axtop2+bxtop+c
Of anders geformuleerd:
De coördinaten van de top zijn:
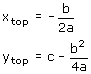
...om maar eens een kort verhaal lang te maken!

vrijdag 8 maart 2002
|
 ©2004-2025 WisFaq
©2004-2025 WisFaq
|