Boom van Pythagoras

Hallo,
Ik moest voor seminarie-wiskunde een werk maken over Fractalen. Ik heb ook een deel dat 'de boom van Pythagoras' behandeld, maar daar heb ik een vraag bij.
Er wordt gezegd op verschillende sites dat , wanneer je een iteratie blijft uitvoeren, de boom maximaal 4 keer zo hoog en zes keer zo breed kan worden dan de zijde van het oorspronkelijke vierkant. Dit kan je ook uitrekenen adhv een rij. Voor de hoogte heb ik reeds de rij gevonden, en de somformule ervoor komt ook uit,nl:

bv. Voor n=20 wordt dit:

s20= 2. (1.1-¹/₂²⁰)/1-(1-2) = 3.99999618… - het nadert dus tot 4.

Nu is mijn vraag, welke rij moet je dan gebruiken om voor de breedte aan 6 te komen? Ik had deze formule eerst gebruikt, maar daar kom ik steeds aan 3 :

Voor n=20 wordt dit:

s20= 2.(1.1-1/3²⁰) = 2.99999999…
1-1/3

Zou jij me kunnen helpen aub?

Elke L
3de graad ASO - zaterdag 27 oktober 2007

Antwoord

Beste Elke,

De Pythagoras-boom is symmetrisch, vandaar dat ik alleen even de linkerkant in beschouwing neem (de totale breedte is dan gewoon het dubbele).



Je ziet dat de breedte te berekenen valt door achtereenvolgens diagonaal + zijde + diagonaal enz. bij elkaar op te tellen.
De vierkanten zijn allemaal gelijkvormig. De rode diagonaal is de diagonaal die bij het vierkant met zijdelengte ¹/₂·Ö2 hoort (want je beginvierkant is 1 bij 1, en door de gelijkvormigheid is zijde_{volgende vierkant} = zijde_{vorige vierkant}·¹/₂Ö2 (Stel. van Pyth.))
Dus de lengte van de rode diagonaal is Ö2·(¹/₂·Ö2) want de diagonaal in een vierkant is Ö2·zijde van vierkant (wederom Pyth.).

De lengte van de gele zijde is (¹/₂Ö2)² want het vorige vierkant had zijdelengte ¹/₂Ö2 en de vergrotingsfactor is ¹/₂Ö2.

De blauwe diagonaal heeft als lengte Ö2·(¹/₂Ö2)³, want de zijdelengte van het vierkant is (¹/₂Ö2)³ en diagonaal = Ö2·zijdelengte.

Als je hiermee doorgaat krijg je



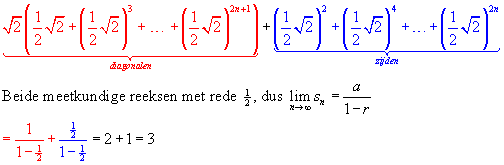
Je zou ook de som kunnen uitschrijven (dan zie je ook dat de lengte van de diagonaal van het volgende vierkant, de zijdelengte van het vorige vierkant is!), dan krijg je halve breedte = 1 + ½ + ½ + ¼ + ¼ + ... en dan zie je dat er halve breedte = 1 + 2·(½ + ¼ + ...) staat oftewel halve breedte = 1 + 2·(^½/_(1-½)) = 3.

Dus de totale breedte is 2·3 = 6.

Groetjes,

Davy.

Vragen naar aanleiding van dit antwoord? Klik rechts..! zaterdag 27 oktober 2007

©2004-2024 WisFaq