Gelijk aantal stemmen onderemingsraad

We krijgen een personeelsvertegenwoordiging in ons bedrijf en daar zijn verkiezingen voor:

We zijn met 43 mensen. Iedereen krijgt 3 stemmen. Je mag niet meer dan 1 keer op dezelfde persoon stemmen. Er zijn 10 kandidaten en 3 zetels te kiezen.

Hoe groot is de kans dat met een populatie van 43 personen die ieder 3 stemmen hebben voor verkiezingen dat bij 10 kandidaten de plaatsen 3 en 4 gelijk eindigen in aantal stemmen?

ChAT GPT maakt er een zooitje van. Dus dat is niet te gebruiken.

NB
Bij de daadwerkelijke verkiezingen hebben we dus echt een gelijk aantal stemmen gekregen voor de nummers 3 en 4 op de lijst en moesten we loten. De kans is blijkbaar redelijk groot .

jeroen
Iets anders - dinsdag 21 maart 2023

Antwoord

Eigenlijk is hier geen sprake van kansen, omdat stemmers niet willekeurig uit kandidaten kiezen. Ik neem aan dat je bedoelt wat de kans is wanneer stemmers hun keuze wel willekeurig maken.

Lastig bij deze vraag is dat het gelijke aantal stemmen voor nummers 3 en 4 op veel manieren tot stand kan komen. Hierin zit weinig systeem, dus het berekenen van deze kans vergt veel losse berekeningen. Ik geef een voorbeeld:

De kandidaten op plaats 1, 2, 3 en 4 noem ik A, B, C en D. Ik start met een overzichtelijke situatie: elke kiezer heeft een stem op A en B uitgebracht (elk dus 43 stemmen). Het grootst mogelijke aantal gelijke stemmen voor C en D is dan 21. De uitgebrachte stemmen zijn dan:
ABC: 21 keer
ABD: 21 keer
ABX: 1 keer (X is een willekeurige andere kandidaat).

De kans dat een stemmer kiest voor ABC is ³/₁₀·²/₉·¹/₈=¹/₁₂₀
De kans op ABD is hetzelfde: ¹/₁₂₀.
De kans op ABX is ³/₁₀·²/₉·⁶/₈=⁶/₁₂₀

De kans dat dit in het gewenste aantal gebeurt, is:



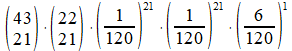
Een tweede mogelijke stemuitslag is:
ABC: 20 keer
ABD: 20 keer
ABX: 3 keer
Voor deze verdeling kan eenzelfde kansberekening worden gemaakt, evanals voor 19 keer ABC, 18 keer ABC enz.

Ingewikkelder is wanneer ABC en ABD 14 keer voorkomen. Dan zijn 15 stemmen over voor X, maar deze mogen niet willekeurig worden verdeeld. Immers, niet al deze stemmen kunnen naar eenzelfde 5e kandidaat E gaan, want dan zou deze kandidaat meer stemmen hebben dan C en D, en zijn C en D dus niet nummer 3 en 4. Nog ingewikkelder wordt het wanneer A en B niet hetzelfde aantal stemmen hebben. Je zult dan nog meer mogelijkheden hebben die allemaal moeten worden doorgerekend. Verder moet er nog rekening mee worden gehouden dat ook andere volgordes dan A, B, C enz. mogelijk zijn waarbij de tweede en derde plaats een gelijk aantal stemmen krijgt.

Kortom, ik begin er niet aan. Handiger lijkt me om een simulatieprogramma te schrijven en de gevraagde kans te bepalen door dit kansexperiment heel vaak te herhalen.

woensdag 29 maart 2023

©2001-2024 WisFaq