Over het projectieve vlak: pool en poollijn

Een vgl van een kegelsnede:

2x²+10xy-14xz+6yz+4z²=0
de rechte l: 5x-4y+3z=0

Bepaal het punt L dat toegevoegd is aan alle punten van rechte tov K (=kegelsnede). (met andere woorden, zoek de pool)

Vraag 1: hoe doe je dat het best?

(We hebben reeds formules gezien voor raaklijnen en zo en poollijnen...)

Vraag 2: in één van mijn pogingen kwam ik tot deze vgl

x·(4·a + 5/2·(3 + 5·a) - 14) + y·(10·a + 6) - 14·a + 1.5·(3 + 5·a) + 8 = 0

dit is de vgl van een rechte, en voor gelijk welke a, gaat deze vgl door één punt, namelijk de pool (1,-1,1). Stel dat ik dit niet weet, hoe kan ik weten door welk punt al die rechten gaan voor gelijk welke waarde van a?

(je kan natuurlijk die a 2 maal een willekeurige waarde geven en dan het snijpunt bepalen, maar da is amateuristisch ;) )

Groetjes

Compug
3de graad ASO - donderdag 10 april 2003

Antwoord

Als er gesproken is over pool en poollijn, dan is vast en zeker de stelling

"de poollijn van een punt op een poollijn gaat door de pool van die laatste poollijn"

ter sprake gekomen.



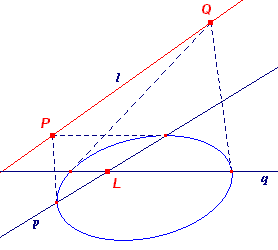
We gebruiken deze stelling.
Bepaal van twee punten (P en Q) op de lijn l de poollijnen.
Het snijpunt L van die lijnen is dan de pool van de lijn l.
Punten op l: P(1,2,1) en Q(5,7,1), met poollijnen
p: 5x + 8y + 3z = 0
q: 19x + 14y - 5z = 0
L (1, -1, 1)
Overigens, met pooltheorie zijn maar weinig amateurs bezig. Wat je dan ook doet, amateuristisch kan het dan zeker niet genoemd worden.
Nb.
Ik heb de vergelijking die je geeft bij vraag 2 verder niet bekeken (daarin ontbreekt trouwens de z).

donderdag 10 april 2003

Re: Over het projectieve vlak: pool en poollijn

©2001-2024 WisFaq