Frostbite

Met de formule F = (2000 - 16,3v)(-5 - T)^-1,688 kan worden berekend hoe lang een mens met onbedekte huid buiten kan zijn voordat frostbite optreedt.

Bij punt c. luidde de vraag: vanaf welke temperatuur is het vanwege frostbite niet verantwoord om een schaatswedstrijd van 10 km met een snelheid van 40 km per uur te laten doorgaan.

Ik kwam zelf op F = 10/40 · 60 minuten = 15. Dus 15 = ( 2000 - 16, 3 · 40 ) (-5 - T)^-1,668. Dus 15 = 1348 · (-5 -T)^-1,668 en daarna liep ik vast. Ik weet niet hoe ik met (-5 -T)^-1,668 moet omgaan.

Joost
Iets anders - maandag 8 november 2021

Antwoord

Als ik het goed begrijp dan gaat het om het oplossen van:

$
15 = 1348 \cdot \left( { - 5 - T} \right)^{ - 1,688}
$

De eerste stap:

$
\eqalign{\left( { - 5 - T} \right)^{ - 1,688} = \frac{{15}}
{{1348}}}
$

De vraag is nu hoe kan je nu weten wat je voor $-5-T$ moet nemen.

De kunst is om van die exponent een $1$ te maken. Dat kan door $-1,688$ te vermenigvuldigen met $\eqalign{\frac{1}{-1,688}}$ en dat betekent dat je links en rechts de macht tot de $\eqalign{\frac{1}{-1,688}}$-ste moet nemen:

$
\eqalign{
& \left( {\left( { - 5 - T} \right)^{ - 1,688} } \right)^{\frac{1}
{{ - 1,688}}} = \left( {\frac{{15}}
{{1348}}} \right)^{\frac{1}
{{ - 1,688}}} \cr
& - 5 - T = \left( {\frac{{15}}
{{1348}}} \right)^{\frac{1}
{{ - 1,688}}} \cr
& - T = \left( {\frac{{15}}
{{1348}}} \right)^{\frac{1}
{{ - 1,688}}} + 5 \cr
& T = - \left( {\frac{{15}}
{{1348}}} \right)^{\frac{1}
{{ - 1,688}}} - 5 \cr}
$

Met een rekenmachine:

$
T \approx {\text{ - 19}}{\text{,4}}^\circ
$

Dat kan...

Maar als je nu toch een GR gebruikt kan je de vergelijking ook wel numeriek oplossen. Op mijn CASIO fx-CG 20 zou ik dat met de solver kunnen doen:



Maar je kunt ook de grafieken tekenen en het snijpunt aflezen:

$
\eqalign{
& Y1 = 1348 \cdot \left( { - 5 - x} \right)^{ - 1,688} \cr
& Y2 = 15 \cr}
$



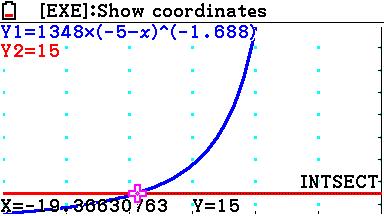
Maar dat is dan weer een heel ander verhaal...
Helpt dat?

maandag 8 november 2021

©2001-2024 WisFaq