Verhouding delen piramide in kubus

Hallo,

Ik heb deze oefening gekregen:

Kubus (ABCDEFGH) met ribbe 4 cm. Daarin zit een piramide (T-ABCD) waarbij T het middelpunt is van het vlak (EFGH) van de kubus. Als M het midden van AE en N het midden van CG dan wordt de piramide in twee delen gedeeld (niet gelijke delen) door het vlak (MNH). Bereken de verhouding van de volumes van de twee delen.

Ik heb de tekening gemaakt, maar weet echter niet hoe ik de volumes van die twee delen kan berekenen, zodat ik de verhouding kan maken.

Heel erg bedankt voor uw hulp!
Liesje.

Liesje
3de graad ASO - zaterdag 17 april 2021

Antwoord

Als ik goed heb ziet die tekening er dan zo uit:



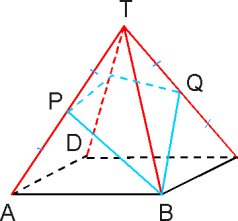
Helpt het als je door P en Q een horizontaal vlak aanbrengt?



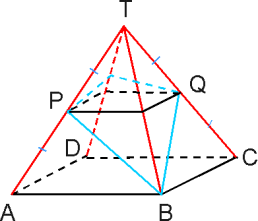
Je krijgt dan twee delen waarbij bij het onderste deel er een piramide met dat horizontale vlak als grondvlak af gaat en er een piramide bij komt. Die delen komen er dan bij de bovenste gedeelte bij en af...

Helpt dat?

zondag 18 april 2021

Re: Verhouding delen piramide in kubus

©2001-2024 WisFaq