Re: Boete krijgen
Ohh, uw bundel gaat me zeker verder helpen! Maar ik vind nog steeds mijn antwoorden niet. Ik weet niet wat ik tussen mijn haakjes moet schrijven en of dit groter of kleiner dan moet zijn.
Dus P(X $<$ ? ) = ? $\to$ dit weet ik dus niet.
En moet ik aangezien het binomiaal verdeeld is een continuiteitscorrectie toepassen?
Om vervolgens b te vinden, hoe moet ik dat doen?
elke
Student Hoger Onderwijs België - zondag 4 april 2021
Antwoord
In de vraag stond toch dat het normaal verdeeld was? De continuiteitscorrectie gebruik je als je een binomiale verdeling wilt benaderen door een normaal verdeling. Het gaat hier om het gemiddelde van 25 onafhankelijk stochasten die normaal verdeeld zijn.
In de lesbrief staan voorbeelden waarbij je een binomiaal verdeling benadert met een normaal verdeling. Je kunt daarbij denken aan munten of dobbelstenen.
De berekening bij b. lijkt sprekend op een van de voorbeelden uit de lesbrief. Je weet de $z$-score, de oppervlakte onder de grafiek en de staandaarddeviatie. Gevraagd wat is het gemiddelde?
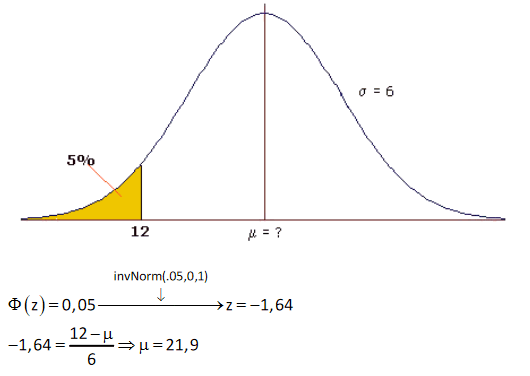
Maak een tekening! Je krijgt dan de volgende berekening:
$
\eqalign{
& P(X < 250) = 0,01 \cr
& \phi (z) = 0,01 \to z \approx - 2,326 \cr
& z = \frac{{250 - \mu }}
{{0,6}} = - 2,326 \cr}
$
...en dat kan je $\mu$ berekenen.
zondag 4 april 2021
©2001-2024 WisFaq
|
Dit is een reactie op vraag 91891