Koordenvierhoek ABCD

Goede middag,
Ik heb een onregelmatige vierhoek ABCD met AB als basis.
Gegeven is:
|AB|=8; |BC|=6 ;|CB|=x en |DA|= 8. De diagonalen zijn : |AC|=11 en |BD|=12 en hoek A=110°
Vraag: bereken de oppervlakte van vierhoek ABCD.

IK ben er al even op aan het zoeken. Tenslotte vond ik een stelling van PTOLEMAUS in een oud meetkundeboek(GOS) die luidt:
Het product van de diagonalen= som van de producten van de overstaande zijden.
Dus : (AC)·(BD) = (AD)·(BC) + (AB)·(CD) Met |CD| = x bekom ik:
(11)·(12) = (8·6) + (8x)
We bekomen: x = (132 - 48)/8 = 10.5
Met de waarde van x kan ik nu verder rekenen.

Driehoeksmeetkunde: S=(a)(b)sin(p)/2

Oppervlakte S(1)(ABD)= (8·8·sin(110°))/2 = 30.0702 cm²

Verder in driehoek BCD werk ik eerst met de cos-regel om de hoek C te vinden:
12² - 6² - 10.5² = -2·6·10.5·cos(A)
cos(A) = -2.25/-126 = 0.0179
arccos(0.0179) = 88°.9744
Ik bereken S(2)= (6·10.5·sin(88°.9744)/2 = 31.4950
Optellen van S(1), en S(2) geeft dan :
S(1)+S(2)=61,5652 cm²
De juist uitkomst zou zijn :
63,305cm² wat iets te veel is Wie is er nu juist ...?

Ik heb wel een TI-40 Collège rekentoestelletje, al vele jaren. Maar die levert niet zoveel decimalen als een smartphone die ik niet in bezit heb. Kan het daaraan liggen of maak ik toch ergens een kleine rekenfout.
Graag wat goede raad als het even kan.
Groetjes,
Rik

Rik Le
Iets anders - woensdag 30 december 2020

Antwoord

Dag Rik,
Ik heb er eerst maar een plaatje bij gemaakt. Dat leest voor een ieder wat makkelijker.



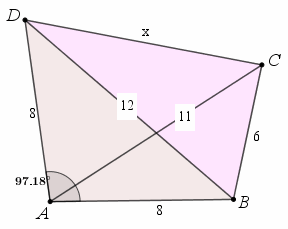
Wat me daarbij opvalt is, dat gegeven is dat hoek A van de vierhoek gelijk is aan 110°. Als ik na constructie die hoek bereken, dan is die waarde 97°,1808.
En dit kan al een verschilletje opleveren met het antwoord.

De door jou gebruikte methode is juist: splitsen in twee driehoeken en dan de S-formule toepassen op elke driehoek.
Bij de berekening van S2 = Opp(BCD) kom ik met een berekening met wat meer decimalen op hetzelfde antwoord als jij.

Het is inderdaad zo dat je "onderweg" de tussenantwoorden beter niet kan afronden, maar als je ziet dat de gegevens in 0 decimalen zijn gegeven, dan is mijn antwoord (afgerond op 1 decimaal) 63,2.

Je hebt volgens mij geen rekenfouten fouten gemaakt. Dus is het door de opsteller van vraag gegeven antwoord (63,3) vermoedelijk onnauwkeurig.

De goede raad? Ga ook in (43 x 47) in gezondheid door met wat je leuk vindt.

woensdag 30 december 2020

Re: Koordenvierhoek ABCD

©2001-2024 WisFaq