Examenvraag mbo 82-83

Ik krijg bij a. een verkeerde hoek bij de volgende opgave:

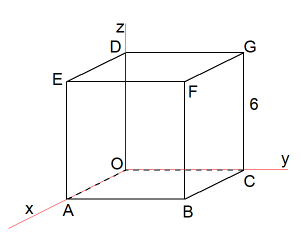
Gegeven zijn de punten A(6,0,0), C(0,6,0) en D(0,0,6). Deze punten zijn de hoekpunten van een kubus OABC·DEFG. Tevens zijn gegeven de punten P(10,0,1) en Q (0,10,6).

1. Bereken de hoek tussen lijn PQ en vlak BGO
2. PQ snijdt het vlak ABF in S en het vlak OCG in T. Bereken de lengte vsn lijnstuk ST.

Voor PQ heb ik l(-2,2,1). Trouwens moet je hier de steunvector gebruiken je hebt m eigenlijk niet nodig toch?

Als ik zo zie dan is het punt B (0,6,6). Voor vlak BGO heb ik l(1,1,0)+m(-1,0,1). Dan heb ik hieruit de normaalvector (a,b,c)=(1,-1,1). En voor de hoek $\Phi$=0,69$\pi$.

Het model geeft 0,2$\pi$.

Hoe ik eventueel aan mijn vectorvoorstellingen kom? De hoek heb ik in mijn uitwerking opgestuurd.

mboudd
Leerling mbo - maandag 20 april 2020

Antwoord

Voor het berekenen van de hoek tussen PQ en het vlak heb je alleen de richtingsvector van PQ nodig:

$
\overrightarrow {PQ} = \overrightarrow Q - \overrightarrow P = \left( {\matrix{
0 \cr
{10} \cr
6 \cr

} } \right) - \left( {\matrix{
{10} \cr
0 \cr
1 \cr

} } \right) = \left( {\matrix{
{ - 10} \cr
{10} \cr
5 \cr

} } \right) \buildrel \Delta \over = \left( {\matrix{
{ - 2} \cr
2 \cr
1 \cr

} } \right)
$

Ik denk dat het $
B(6,6,0)
$ moet zijn.

$
n_{BGO} = \left( {\matrix{
1 \cr
{ - 1} \cr
1 \cr

} } \right)
$

Dat klopt!

$
\eqalign{
& \cos \phi = {{\left| {\left( {\matrix{
{ - 2} \cr
2 \cr
1 \cr

} } \right) \cdot \left( {\matrix{
1 \cr
{ - 1} \cr
1 \cr

} } \right)} \right|} \over {\left| {\left( {\matrix{
{ - 2} \cr
2 \cr
1 \cr

} } \right)} \right| \cdot \left| {\left( {\matrix{
1 \cr
{ - 1} \cr
1 \cr

} } \right)} \right|}} = {1 \over 3}\sqrt 3 \cr
& \phi \approx {\rm{0}}{\rm{,955316}}... \cr
& \varphi \approx {1 \over 2}\pi - {\rm{0}}{\rm{,955316}}... \approx {\rm{0}}{\rm{,6154}}... \cr
& \varphi \approx {\rm{0}}{\rm{,20}}\pi \cr}
$

Helpt dat?

maandag 20 april 2020

Re: Examenvraag mbo 82-83

©2001-2024 WisFaq