Constructies van vijfhoek en zeshoek

Gegeven zijn een geheel getal $n$ groter of gelijk aan 3 en een serie $M_1$, $M_2$, $M_3$, ... $M_n$ van $n$ punten in het platte vlak.

Bestaat er een n-hoek $P_1P_2P_3...P_n$ waarvoor geldt dat de n gegeven punten $M_1$, $M_2$, $M_3$, ... $M_n$ achtereenvolgens de middens van de n opeenvolgende zijden van die $n$-hoek zijn (met andere woorden $M_1$ het midden van zijde $P_1P_2$ is, $M_2$ het midden van zijde $P_2P_3$, …etc)? Zo nee, waarom kan dat niet? Zo ja, hoe wordt het dan gevonden? En is er een unieke $n$-hoek of zijn er meerdere mogelijkheden?

Maar als je bijvoorbeeld wel $P_1$ zou weten, hoe zou je de vijfhoek dan kunnen reconstrueren? En wat gebeurt er als je $P_1$ net even ergens anders kiest? Gaat het dan nog steeds goed?

Ik heb 5 middens gekozen. Zie aub bijlage. Ik ben niet sterk in GeoGebra helaas. Ik heb geprobeerd maar lukte mij niet helaas. Hoe zou ik dan die middens een vijfhoek tekenen. Hier loop ik vast.

Bijlage

M
Student hbo - vrijdag 10 april 2020

Antwoord

Bij gegeven punten $M_1$ t/m $M_5$ zou je een willekeurig punt $P_1$ kunnen kiezen. Vervolgens kan je met puntspiegelen de andere punten tekeken. Uiteindelijk moet je dan bij het laatste punt uitkomen op $P_1$.

Ik heb de volgende punten gekozen:

$
\begin{array}{l}
M_1 (1,0) \\
M_2 (5,1) \\
M_3 (4,4) \\
M_4 (1,5) \\
M_5 ( - 2,3) \\
\end{array}
$

Als je dan $P_1(-2,0)$ kiest als eerste punt dan komt je uiteindelijk niet uit op $P_1$. Dat zou ook wel heel toevallig zijn.



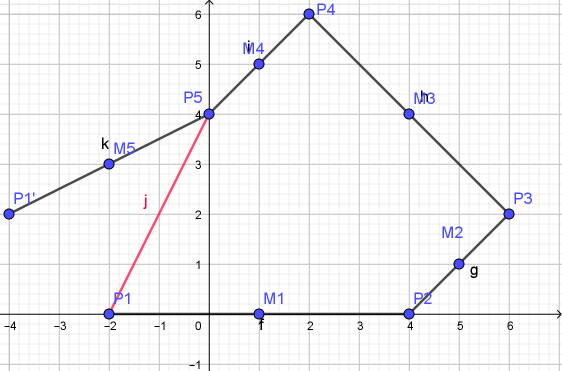
In GeoGebra kan je $P_1$ verslepen zodat je wel weer mooi op $P_1$ terecht komt.



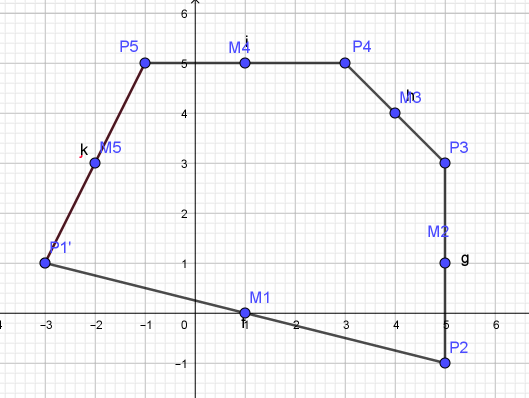
Dat blijkt het punt $(-3,1)$ te zijn. Dat moet je dan ook wel kunnen berekenen!

Is dat wat je bedoelt? Kan je er mee verder?

zondag 12 april 2020

Re: Constructies van vijfhoek en zeshoek

©2001-2024 WisFaq